The physical distance between Europe and North America is perhaps a few thousand kilometers but from a acid base point of view, we are talking light years. It is sad that acid-base (which should be relatively easily understood, now that we have modern computers to do the dirty work for us) is plagued by unnecessary argument. Particularly vituperative comments have come from Severinghaus and Siggaard-Andersen, criticising the work of Stewart and the "strong ion difference" concept. We believe that although Siggaard-Andersen has made a massive contribution to the understanding of acid-base, Stewart has provided a sound mathematical approach which is of great use in understanding acid-base. This article briefly examines Peter Stewart's approach to acid-base. It's best read carefully, but you can jump straight to the calculator, a Java applet that implements his model!
This web page makes few assumptions about your knowledge. It should be easily understood by anyone with a high-school education and a bit of a background in clinical medicine and physiology. We try to keep things simple - if you feel that our tone is patronising, then you are probably too advanced to be reading such simple stuff! Note that a bit of spadework is still required to work through the maths - pen and paper remain a wonderful medium for this! Because solutions for the more complex equations require the use of computers, we use a tiny little bit of "computerspeak" - as little as we can get away with! We do however feel obliged to use a star (*) to indicate multiplication and a slash (/) for division. This page does not assume that you can speak a computer language.
Remember from physiology that if you have two substances A and B reversibly combining to form substance C, that when the reaction is at equilibrium the equation governing the equilibrium is:
where K is the rate constant for the reaction.
Throughout the body pH is vitally important. Anyone who has a blood pH of below 7.0 is likely to die soon if this isn't corrected. Likewise, a pH of over 7.6 is frequently associated with serious illness and death. Remember that pH is the log of the reciprocal of the hydrogen ion concentration. Why use such a convoluted measure, and not just talk about the concentration of hydrogen ions? The answer is mainly historical but also perhaps reflects the ongoing inability of humans to cope with concepts that cannot be counted on fingers (with perhaps a little help from the toes)! Rather talk about pH 7 than 1 * 10-7 mol/litre, or (god forbid!) 100 nanomol/l of hydrogen ion.
Unfortunately, such terminology has only served to complicate things, especially when we start plotting how pH changes when we change another ion concentration - we have to continually remember that we are dealing with non-linear axes on any graph we might draw. We will try and clear up some of the confusion. It goes without saying that in any solution mass is conserved (the amount of each component remains constant unless some of that substance is added or removed, either physically or by participating in a chemical reaction), and that any aqueous solution is electrically neutral (the number of positive ions equals the number of negative ones). But let's review a few other fundamental definitions:
Here is a list of common strong ions (in biological solutions):
In all biology, approximations are necessary. Although each of the perhaps 1014 cells in the body is unique, we can define groups of cells and treat them as single entities. Likewise, we have identifiable subsets of body fluids that we can define and analyse. Important components are
Water is weird. This weirdness is the basis of life. Among its most peculiar characteristics are:
The last statement deserves a bit of explanation. Because water molecules are small (molecular weight of just 16+1+1 = 18) the molar concentration of water is enormous - about 55.3 mol/litre at 37 degrees C. There are a billion times fewer hydrogen ions than there are water molecules in a glass of water. Remember that even the hydrogen ion is a convenient fiction - it's just a simple symbol (H+) for a statistically very complex association between a proton and a whole lot of surrounding water molecules that the proton finds very attractive. The life of the common proton is far more complex than even the most Byzantine modern TV soap opera!
Water dissociates as follows:
This is a very rapid reaction indeed, and we will always assume that equilibrium is reached instantaneously in biological solutions.
At equilibrium, the following equation must hold:
As we've already implied by saying that water doesn't dissociate very much, the dissociation constant KW is rather small, in fact, about 4.3 * 10-16Eq/l at 37o Celsius. This is really tiny. Also note that KW varies rather remarkably with temperature - for example at 25 C it is about 1.8 * 10-16Eq/l ! If you're smart, you'll immediately realise that the pH of a glass of water changes dramatically as its temperature changes! Further contemplation will also assure you that we can assume a new constant
As an aside, you can approximate the value of KW' by:
KW' = 8.754 * 10-10 * e(-1.01*106) / T2)
where temperature T is expressed in degrees Kelvin
From the above we know that
A solution is basic if [H+] < ROOT (KW')
Take some water. Add strong electrolytes, such as NaOH and HCl, which we know will almost completely dissociate. We now have a heady mix of water, Na+, Cl-, H+ and OH- ions. What will happen to the hydrogen ion concentration in this mix?
We already know that water dissociation constrains us to:
If SID is positive and bigger than about 10-6 Eq/l you can see that KW becomes insignificant, and Equation #3 becomes very nearly the same as:
If the SID is negative and bigger than about 10-6 Eq/l then Equation #2 simplifies out to: [H+] = -[SID] but such solutions are not commonly encountered in biological systems.
"Okay, this is all very well" you say "but what is the practical significance of all this maths?" Easy. The above tells us that in a solution containing strong ions, if you want to calculate the pH, you must:
You can also see that if we have (for example) an acidic solution and we progressively add base, there will be a sudden, rapid rise in pH as we approach the point where [SID] is zero, and then add just a tiny bit more base. Consider the following diagram (our applet) showing how pH changes with SID - Press the button!
pH is easily measured so now we finally understand the concept of "titratable acidity" of for example urine (we add base until there is a sudden rise in pH and this is the point where "titration is complete" - that is, the SID of the solution is zero). But remember that this doesn't tell us what titratable acidity means, and also note that the "sudden change in pH" is an artefact induced because pH is logarithmic: nothing that dramatic happens if we look at actual hydrogen ion concentration! Try this - in the above applet, change the Y axis parameter from pH to [H+] and press on the Calculate button again!
It is instructive to read Stewart's book where he looks at titration of interstitial pH using HCl - the counter-intuitive nature of pH is clearly seen.
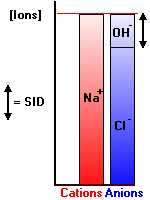
Electrical neutrality in solution demands that Equation #1 is satisfied - the sum of [negative] and [positive] ions is always zero. This is conveniently represented by two adjacent bar plots as shown in the following illustration (after Stewart, p43).
The solution is a simple one containing [H+], [OH-], [Na+] and [Cl-]. The bar plot (Gamblegram) clearly shows the disposition of ions. The minuscule amount of H+ ion is not shown. Such plots can be used for far more complex solutions, often with unmeasured ions (where the term "gap" is often used, as in "anion gap"). It is crystal clear from the plot that the SID is equal to the amount of hydroxyl ion. In alkaline solutions the SID will be positive, in acidic, negative.
Adding a weak electrolyte (one that only partially dissociates in the pH range we are considering) complicates things rather a lot. In body fluids such as plasma, the most important weak electrolyte is albumin, but the principles hold for all weak electrolytes.
As above, we can work things out if we have the correct numbers, and plug them into the relevant equations. Two of the equations we already know, those governing the dissociation of water and the requirement for electrical neutrality (slightly modified to include the dissociated anion A-, derived from the acid):
[H+] + [OH-] + [SID] + [A-] = 0 .. Equation #1A
[HA] + [A-] = [ATOT] .. Equation #5
Unfortunately for people such as myself who are used to counting on their fingers, the solution of the above four equations is based on cubic equations. Fortunately, when we use digital computers to solve such equations, the difficulty evaporates! We explore this below. When we actually go to the bother of solving the equations, we reach several initially rather counter-intuitive conclusions.
Click on Calculate and then change the Albumin value to say 40, and click once more. The difference between the two curves is clearly seen - albumin only really has an effect between an SID of zero and an SID of about 0.02. (An albumen of 40 g/litre more-or-less corresponds to an ATOT of 0.016 Eq/l, perhaps a bit less)!
Click on the above graph to get the picture with an albumin of 40g/l, and then decrease the albumin to 0 and click again - notice how the new, red, albumin-free graph changes LESS steeply! Wham!
|
WE MUST KNOW ALL THE INDEPENDENT VARIABLES IN ORDER TO CALCULATE THE DEPENDENT ONES! |
Calculations for a weak base are similar to the case of the weak acid above. In an analogous way, added weak base is most effective in the SID range zero to -[BTOT]. The difference is that buffering here does occur: the base flattens the [H+] versus [SID] curve very effectively!
If you've successfully come this far, the following section should not be beyond your capabilities, even if computers scare you witless! You may however skip the following computerese. If you choose to read it, then also get a piece of paper and write down the equations, and work things out. We take the equations from above:
[H+] + [OH-] + [SID] + [A-] = 0 .. Equation #1A
[H+] * [A-] = KA * [HA] .. Equation #4
[HA] + [A-] = [ATOT] .. Equation #5
[HA] = [ATOT] - [A-] (from Equation #5)
and by substituting the latter into Equation #4,
[A-] = Ka * [ATOT] / ( [H+] + KA )
One can sit down and turn the above into a third order polynomial, but because we are simple-minded people, we will abbreviate it to:
Look at Equation #6 carefully - assume we know the value of [H+]. If we fill in this value, then the left hand side of the equation will be zero (of course). But let's say we are not quite sure of [H+]. We guess its value. Plug this guessed value in, and we find something very exciting - if the guessed value is too big, then when we plug in the value, the result is positive. And if the guess is too small, the result is negative. From the sign of the result, we know whether our guess was too big or too small. We have a way of testing our guesses! Even better, if we have a guess that is too big and one that is too small, we know that the true value must be somewhere in between, so we can progressively narrow down the true range within which our target lies. We will never quite reach a "true" value for [H+], but we can get as close as we jolly well like, effectively conquering our cubic equation!
Many people are terrified of computers - an unnecessary state of mind, as all computers do is give us a way of implementing an algorithm like the one above in a fast and accurate way! In order to implement our algorithm we need to express it in an unambiguous way. We use statements written in a computer language to do so.
We will now 'formalise' the above algorithm. We won't yet write it in a specific computer language, we will just make things more precise, without (we hope) compromising readability. Our only assumptions are:
If you were unwise enough to read the above in one sitting, we suggest that you take a tea break to marshal your resources!
Remember the fundamentals:
People who are familiar with acid base as it is commonly taught, usually cut their teeth on the Henderson-Hasselbalch equation. There is little wrong with the H-H equation, other than the fact that it only represents part of the truth. Here we start to explore how carbon dioxide behaves, but in what we regard as the proper context. Much of the following may seem familiar, but be careful - don't lose sight of the big picture!
Take our familiar mixture of strong ions and water, and expose it to CO2. What happens? Four things can happen to CO2 gas when exposed to water - it can dissolve, react with water to form carbonic acid, or even form bicarbonate or carbonate ions. We will explore each of these in turn, but the two most significant reactions are the formation of carbonate and bicarbonate, as each has its own equilibrium constant. By now you will realise that these reactions with their equilibrium constants will have a profound influence on the whole system, and it is only in the context of the whole system that we can understand the role of carbon dioxide. Let's see:
Forward Reaction
|
Reverse Reaction
|
| ===> Depends on partial pressure of CO2 | <=== Depends on concentration of dissolved CO2 |
| Rate of forward reaction = Kf * PCO2 | Rate of reverse reaction = Kr * [CO2 (dissolved)] |
..AT EQUILIBRIUM..[CO2(dissolved)] = SCO2 * PCO2 .. Equation #7A For Kf/Kr we have substituted SCO2, otherwise called the Solubility of CO2. In other words, the amount of dissolved CO2 depends on the partial pressure of CO2 times a rate constant. SCO2 is dependent on temperature, and at 37 C it is about 3.0 * 10-5 Eq/litre/mmHg. Note that if we are examining a fluid that isn't in contact with gas, we still talk about a partial pressure of that gas in solution "as if" it were exposed to, and in equilibrium with, a gas containing that gas at that partial pressure. This is just another convenient way of representing the concentration of dissolved gas in solution. |
|
| Equilibrium is represented by:
[CO2(dissolved)]
* [h30] = K * [H2CO3]
.. Equation #7B
|
|
If we treat [h30] as constant, and rearrange things a bit we get:
[H2CO3] = KH * PCO2
The value of KH at 37 C is 9 * 10-8 Eq/litre - because of this, the H2CO3 concentration is far smaller than the amount of dissolved CO2. |
The reaction of CO2 with water is
SLOW , with a half time of about 30 seconds, fortunately
speeded up to microseconds by the carbonic anhydrase abundantly present
in most tissues.
| Equilibrium is represented by:
[H+] * [HCO3-] = K * [H2CO3]
It follows that: [H+] * [HCO3-] = KC * PCO2 .. Equation #8 A good value for KC is 2.6 * 10-11 (Eq/l)2/mmHg. |
| Equilibrium is represented by:
[H+] * [CO32-] =
K3 * [HCO3-]
.. Equation #9
A typical value for K3 is 6 * 10-11 Eq/litre. |
As usual, we need four simultaneous equations to work out all the dependent variables (given the independent ones). These are our old familiar equation #0, Equations #8 and #9, and the requirement for electrical neutrality:
[H+] * [HCO3-] = KC * PCO2 .. Equation #8
[H+] * [CO32-] = K3 * [HCO3-] .. Equation #9
[SID] + [H+] - [OH-] - [HCO3-] - [CO32-] = 0 .. Equation #10
It is important to distinguish between dependent and independent variables. Bicarbonate concentration and hydrogen ion concentration are dependent variables, but SID and pCO2 are independent!
We work out our equation for [H+] in the same way we did in Section 3 above, and solve it using a computer, again as above. On contemplating the results thus obtained, a whole host of interesting conclusions emerge. These include:
The combination of strong ions, carbon dioxide and a weak acid closely models blood plasma, but also provides a fairly accurate representation of intracellular fluids. Blood plasma is rich in weak acids, the majority being proteins. For the purposes of analysis it is probably moderately accurate to regard them as being all one acid with a single ATOT and single KA. This assumption is not however central to Stewart's work - as is seen in the articles by Figge et al who extend his model with multiple Ka's.
Following the pattern we established in previous sections, we
identify the independent variables ( [SID],
PCO2, ATOT which
are respectively the strong ion difference, partial pressure of CO2
and the total amount of weak acid present). In addition, we need to know
KW', KA, KC and K3. Given these,
we can calculate any one of eight dependent variables:
HCO3-, A-, HA, CO2
(dissolved),
CO32-, H2CO3, OH-,
and H+. Note that dissolved CO2 and H2CO3
are easily determined from Equations #7A and #7B.
Exactly as we have done before, we derive six simultaneous equations, most of which are old friends:
[H+] * [A-] = KA * [HA] .. Equation #4
[HA] + [A-] = [ATOT] .. Equation #5
[H+] * [HCO3-] = KC * PCO2 .. Equation #8
[H+] * [CO32-] = K3 * [HCO3-] .. Equation #9
and finally, to maintain electrical neutrality:
[SID] + [H+] - [HCO3-] -
[A-] - [CO32-] - [OH-]
= 0
Try experimenting further with our Java applet for blood plasma. This applet uses the above equation and iterative approach. First, simply press the "calculate" button. Then play - try seeing what happens to pH as you vary the SID and Albumin level. Then change the independent variable (on the X axis). Later you can see how other dependent variables (eg CO3--) change with variations in e.g. pCO2.
ionz - Copyright (C) J van Schalkwyk, 1999
I'd like to thank everyone for their feedback (mainly positive) about
this page, particularly Rinaldo Bellomo and
John Kellum, who have
contributed enormously to spreading the news about the physicochemical
approach, and also Jon Waters, and
Philip Watson.
A good website that explores both the traditional, and now the Stewart approach,
is that of Kerry Brandis.
Thanks too to PJ Hilton, who pointed out a typo in Stewart's book, which we carried over in a mildly embarrassing fashion.
Recent developments are explored on yet another page on anaesthetist.com. Further constructive comment is of course still welcome. By the way the actual distance between Brown University (Stewart) and Copenhagen (Siggaard-Andersen) is 5958 km, just for the record.
It's a tragedy that Peter Stewart is dead - the man was a genius}
| Date of First Publication: 1999 | Date of Last Update: 2006/10/24 | Web page author: Click here |