How echocardiography worksEchocardiography provides a picture assimilated from the faint echoes that arise when short pulses of high frequency sound (ultrasound) are passed through tissues. The computation needed to produce quality pictures is non-trivial, but the fundamental principles can be understood by anyone with a high-school education.FundamentalsConsider an ultrasound transducer. This is usually a piezoelectric crystal - a crystal with the peculiar property that, when voltage is put across it, it deforms ever so slightly, and that when it is deformed (ever so slightly!) the voltage across it changes. A little thought will lead one to the deduction that if one varies the voltage across the crystal, a sound wave will be generated, as all sound really is is a pressure wave that passes through a medium. A crystal that is repetitively thickening and thinning out again must cause local changes in pressure - a sound! What is really sneaky is that reflected sound will cause a minuscule distortion when it strikes the crystal, and the consequent change in voltage can be picked up and interpreted. The timing of this echo will give us an indication of the depth at which it occurred, in the same way that German submarines were detected and their distance estimated by wartime sonar (sound navigation and ranging).In TOE, we commonly use sound waves with a frequency of 2.5 to 5 million cycles per second (megaHertz), or more. This is well above the upper range of normal human hearing, which in children is perhaps 20 kiloHz, and in senescent adults drops considerably below this. What is the relationship between frequency and wavelength?Why do we use such high-frequency sound in echocardiography? If you want to "see" a tiny object with sound, you will need sound that has short wavelengths. This is why bats use such high frequency sound. Now, within the heart, we are interested in resolutions of perhaps a millimetre or less, so it makes sense that we need short wavelengths. Consider a sound with a frequency of 5 MHz passing through water (or human tissue). Sound passes through soft tissues at almost exactly 1540 metres per second, so 5 Million cycles will fit into 1540 metres. From this we can work out the wavelength, which is simply the distance between one peak of sound intensity and the next - here 1540 metres / 5 000 000, or about 0.3 millimetres. You can also work out the general formula that relates velocity, frequency and wavelength:
v = f *
Also note the simple relationship between the time interval from one crest
to another (lets call this
.. and the relationship between velocity and distance travelled (
Imagine a beam of ultrasound passing through a tissue. Part of the beam will be attenuated (absorbed by the tissue), part will be reflected, and part will be scattered. We call the reflected part specular echoes - these are the components that we are interested in, while the scattered beam merely serves to confuse us! Scatter is worse in tissues that are inhomogeneous at a microscopic level, while specular reflection occurs mainly at interfaces between tissues of different density. For example, a beam passing through the point where blood meets, say a papillary muscle, will be strongly reflected at this point, provided the size of the reflecting object is at least a quarter of the wavelength of the ultrasound. There is a trade-off - we pick up smaller objects more easily with shorter wavelengths, but as we shorten the wavelength, scatter worsens, increasing our confusion! In addition, as we shorten the wavelength (raise the frequency) of an ultrasound beam, we impair its tissue penetration. How is sound attenuated in various tissues?Different tissues differ dramatically in their ability to transmit sound. We usually talk about the "half-power distance", which is the depth at which the sound is halved. Here are some examples:
You can see that there will be minimal transmission of ultrasound through lung and bone, and that even muscle attenuates the beam dramatically. This is the main reason for the superiority of TOE over transthoracic echo - there is just too much attenation with TTE due to the presence of chest wall and especially, lung tissue. TimingA beam of ultrasound moves fairly rapidly through tissue - 1540 m/s is far from sluggish! If you wish to interrogate tissues to a depth of say 15cm, the beam can get there and back in 0.150/1540 seconds, that is, 195 microseconds. This gives us the opportunity to send out multiple pulses of sound every second, and obtain a dynamic picture of what is going on in the tissue. For example, we might send out just three pulses at a frequency of 5 MHz, and then listen for about 250 microseconds, mark time for 750 odd microseconds, and then send out another set of pulses, and so on.If we display on a screen the echoes coming back from one set of impulses, the picture isn't very informative. The Y axis will tell us how deep a particular echo is, and more intense echoes will be brighter, but the single line will be difficult to interpret. But if we draw successive lines on the screen, as each packet of information comes in, we get a motion display, usually abbreviated to M-mode. From the M-mode image we can precisely determine depths and therefore dimensions (and changes in dimensions) of structures. It's often quite easy to interpret which structure we're looking at on M-mode, but of course our task is made easier by modern technology, where we usually look at a two-dimensional image, and then simply indicate where we want our M-mode 'slice'. How do we obtain two-dimensional images? Two-dimensional ImagesEarly two-dimensional echo probes had a rotating head. This allowed beams of ultrasound to be fired off at various (continually changing) directions, and the returning echoes provided information that could be reconstructed into a two-dimensional picture of the tissue being interrogated.Current imaging is more subtle. Probes consist of an array of parallel piezoelectric elements - often sixty four or more of these. We use trickery to produce a wave-front that moves in a certain direction - if all of the piezoelectric elements fire at the same time, then a wave front will be formed from all of these little elements, and it will move off parallel to the plane of these elements. But what happens if we fire first one element, then the next in line, and so on? If you sit down and draw this, then you'll soon see that the wave front will move at an angle to the line of the piezoelectric array. This trick can be used to move the angle of the wavefront through ninety degrees (practically, although the theoretical maximum is a full 180o), so multiple beams can be used to scan a ninety degree sector of tissue. Returning echoes are then re-constituted into a 2-D picture. Because of the rapid return of the echoes, a full image can be captured about every sixtieth of a second, and images can then be displayed to give an impression of continuous motion (two images are usually interlaced, so the 'refresh rate' of the image you see on the screen is usually about thirty times per second). What determines the resolution of a picture?In a two-dimensional image, there must be two different resolutions, the "side-to-side" (lateral) resolution being determined mainly by how narrow the beam is (assuming the wavelength is appropriate), and the resolution along the length of the beam (axial resolution) by frequency and number of pulses (The higher the frequency, the better the resolution, the more pulses you send, the more 'things get confused' and the lower the resolution). The axial resolution is approximated by:Raxial = 0.77 * Npulses / f where R is resolution in millimetres, Npulses is the number of pulses, and f is the transducer frequency in MHz. For a 5 MHz transducer and 3 pulses, the resolution works out at about half a millimeter. Lateral resolution is far worse - generally about 2 mm. How deeply can we look?The major factor that limits the depth to which an ultrasound beam can interrogate a tissue (apart from attenuation) is related to beam divergence. Even the "flattest" wavefront that originates from a transducer tends to diverge with distance (To use an optical analogy, even the most tightly collimated laser beam is half a kilometer wide when it reaches the moon)! The "depth of field" (the distance at which the beam is no longer parallel) is estimated by: L = (Ltransducer) /
Where L is the depth of field, Ltransducer is the size of
the transducer, and
Pre-processingA variety of filters and compensatory adjustments can be made to the incoming signal. These include:
Post-processingThe digitised image obtained from even the most sophisticated transducer is actually rather unattractive, and full of holes. Extensive post-processing is used to render the picture more attractive and intelligible. The radial information is transformed into a raster image (rectangular image made up of dots), commonly made up of about 65 000 or more picture elements (pixels). The image is grey-scale (varying shades of grey), with up to 1024 shades of grey stored in the memory of the echo machine, although fewer shades are usually shown on the screen! Other tricks include:
The principles of Doppler echocardiographyThe basic idea behind the Doppler effect is simple - as usual, the devil is in the details. We all know how an ambulance siren appears more high pitched as the vehicle moves towards us, and then wheee..ooooh becomes more bass as the flashing red light vanishes into the distance. Clearly if an object that is stationary relative to you is emitting sound at a frequency f, the interval between pulses will be 1/f seconds. But if the object is moving directly towards you and emits a pulse, it will have caught up slightly with this pulse at the time it emits the next pulse, so the frequency of the sound will be boosted. Similarly, if an object moving towards you reflects a sound you have emitted, it will raise the frequency (pitch) of the sound it reflects. Let's look at this in a little more detail.. (or you may wish to skip straight to the Doppler equation)!Consider a doppler probe emitting a continuous stream of ultrasound towards a column of blood heading directly towards the probe. The oncoming red blood cells will reflect some of the sound back towards the probe. Let's find out how we can calculate the velocity of the blood flow, knowing the change in frequency of the reflected beam. Some basicsFirst of all, we need to set some ground rules. Don't be intimidated by the symbols - they're all pretty well self-explanatory. We will often refer to the following, so let's make them quite clear:
Sorting out the Doppler EquationNow let's attack the Doppler equation. Our goal is to find out the velocity of a column of blood moving towards a Doppler probe, if we know the change in frequency of the reflected ultrasound beam. Consider the following picture:
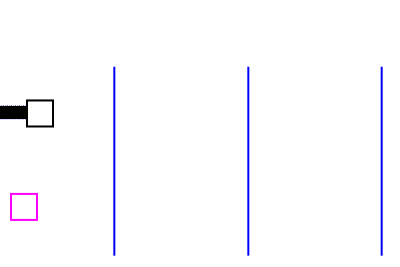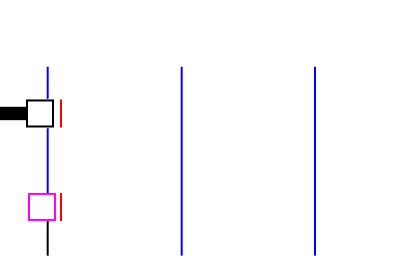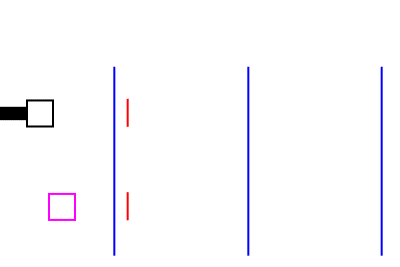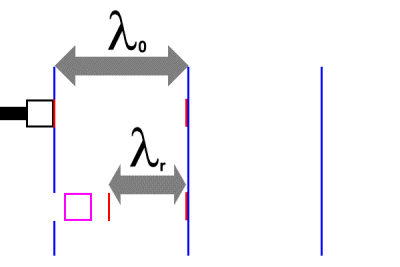
The stationary black block in the above diagram simply reflects the sound, and the frequency of the reflected sound is the same as that of the incoming beam, that is, fout. The moving magenta block (or red cell, if you wish) is quite different. At some point, the moving cell will encounter a wave crest, and reflect the wave. The cell will then carry on moving, and therefore will encounter the next wave crest sooner than if it were stationary. Can we calculate how long it will take for the moving cell to meet the next wave crest? Certainly.. In the time that it took the cell to meet the next wave crest, the
cell has moved towards the wave crest with velocity vcell, and
the wave crest has moved towards the cell with velocity vsound.
The total distance the two have moved before they collide is clearly
the distance between oncoming two wave crests, which is Now, we know that vcell *
Rearranging, we find that Think carefully now..As we've mentioned, the red cell reflects first one and then a second crest. Consider the distance between the first reflected crest and the second one. In the time ( t) it takes for the cell to encounter the second pulse,
the first pulse has moved a certain distance back towards the ultrasound
probe. But wait a bit! Because the cell is moving in the same direction
as the reflected sound, the cell partially catches up with the beam it reflected!
How do we take this into account? Easy. At the instant we are considering,
the distance between the cell and the
reflected wave (which is the same as the wavelength of the reflected beam) is simply
the distance travelled by this wave front minus the distance travelled
by the red cell in the same time. Knowing that distance equals velocity times
t, we see that:
In other words, we need to subtract the distance travelled by the red cell in the same direction as the reflected crest. We can now easily work out the frequency of the reflected sound. First, we rearrange Equation 3.1, thus: Then we substitute the value we obtained for Using our knowledge of the relationship between frequency and wavelength, we can easily rearrange this to: vsound / fr = vsound / fout * (vsound - vcell) / (vcell + vsound) .. Equation 4.2 Cancelling the vsound and rearranging, we get a formula for the frequency of the reflected beam.. fr = fout * (vsound + vcell) / (vsound - vcell) .. Equation 4.3 Look at the above equationDoes Equation 4.3 make sense? Yes. The reflected frequency will be boosted, as we expect. (The police siren is more shrill as it approaches us). Conversely, if the magnitude of vcell is negative, the frequency will be lowered. It's now easy to rearrange our equation to solve for vcell:fr * (vsound - vcell) = fout * (vsound + vcell) vcell = vsound (fr - fout) / (fout + fr) If we abbreviate (fr - fout) to equal " vcell = vsound * When we're dealing with physiological blood flow, the change in frequency
is small compared to fout (This is because the velocity of blood
flow is maximally a few metres per second, which is trivial compared with
the 1540 m/s speed of sound in water). So we conveniently ignore the
vcell An important complicationNote that in the above we assumed that the column of blood was headed directly towards the Doppler probe. In real life, this is by no means always the case. We need to be very careful, because gross errors (underestimates) can occur if we don't realise that the above principles only apply where blood flow is in the line of the probe - either towards or away from the probe. The Doppler shift of blood flowing at right angles to a probe is always zero! Fortunately for us, it's easy to compensate for small errors in probe angulation. Consider blood flowing not directly towards a probe, but at an angle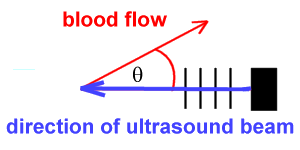
to the orientation of the probe:
Only the component of the blood flow directed towards the probe will be measured. If the true vector is away from the direction of the ultrasound beam, then: cos We thus compensate by saying:
The above is the 'true' Doppler equation for sound reflected
from a moving object, where vcell is the velocity of the
object moving towards the probe, fout is the sound frequency
emitted by the probe, vsound is the velocity of sound in
water (1540ms-1), and ApplicationsHere we plan to have a section on actual doppler images, and Doppler assessment. It will be a long time before we can achieve this goal! | |||||||||||||||||||||||||||||
.. Equation 1.1
vsound *