An introduction to Binary Logic
(What part of 'No' don't you understand?)
|
If you're one of those people who wants to know a little about logic,
but whose temperature is not significantly increased above -273.15oC
by terms such as "modus ponens", "metalogical variables", and "equivalence
transformation", this page may be for you! Logicians particularly
have been guilty of 'epistemology', which could cynically be defined as
'arguing about made-up words to the discomfort of others'! We've provided
a glossary and index at the end of this document, as it's probably best
to read the whole thing, your first time around!
Introduction
If you know even a tiny 'bit' about digital computers, you know that they
"work on 0's and 1's". Let's tie this up with logic. We'll set a few
ground 'rules':
|
Rule 1 |
|
In binary logic, we're only concerned with whether something is
TRUE or FALSE.
|
|
Rule 2 |
|
If something is TRUE, we will regard this as being synonymous with
a value of "1", and FALSE will be considered synonymous with "0".
|
There is no reason why we have to use 0 for False, and 1 for True.
It's entirely arbitrary.
We could have said that "red" is synonymous with FALSE, and "green"
with TRUE, but out of deference to those with red/green colour blindness
we'll stick to zero and one)!
Let's now consider two tiny little containers, into which we can squeeze
either a 0 or a 1. We can invent a fancy name for these two containers.
Each one we will call a "binary digit" or "bit". Each of the two bits
can contain the value 0 or 1. Another way of saying this is that
each bit is a variable, which has two possible values - zero or
one. From this small basis, we'll progressively build up a whole
logical 'system', called the Propositional Calculus. But before
we do so, remember that within computers, not only can we store bits,
we can also send them along wires. Computers commonly represent a "0"
as a certain voltage on a wire, and a "1" as another, distinct voltage.
Two bits taken together
Digital computers can simply be considered as devices that manipulate
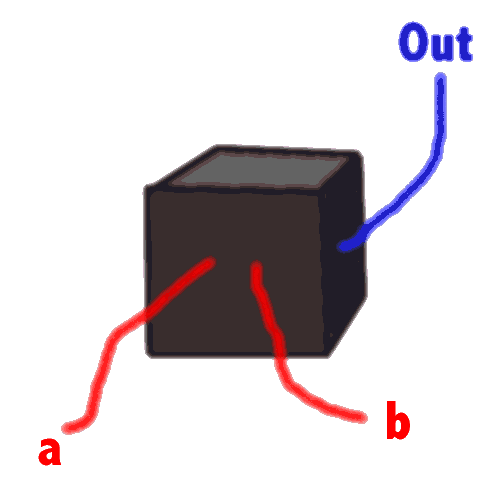
bits. Let's consider a computer to be a black box. For
the sake of simplicity, let's assume that our black box has only two
wires going in, and one wire coming out (What could be simpler?)
We can somehow 'put' either a 0 or a 1 onto each wire simultaneously,
and - Voilá - after a very short delay we get a result - either
a zero or a one, on the wire coming out! Here's our box:
Think about this setup. It's actually rather complex. For the inputs
a and b
can each have the value zero or one, and for each of these four possible
combinations (00, 01, 10 and 11), there is the possibility of the result being either
zero or one! Let's assume that whenever we put the same values
in on a and b, we get the same value Out.
Now, 'at random', let's choose one of the possible things that
might happen.
We might find that:
- If a is 0 and b is 0, the result is 0;
- If a is 0 and b is 1, the result is 1;
- If a is 1 and b is 0, the result is 1;
- If a is 1 and b is 1, the result is 0.
How many other possible patterns can you see?
Truth Tables
Yep. The answer is fifteen other patterns (a total of sixteen).
We have a convenient way of representing the actual outcomes. It's
called a truth table. Here's our example:
| |
Value of a
|
| False
| True
|
| Value of b |
False
| 0
| 1
|
| True
| 1
| 0
|
You can work out how to read the above - for example, if a is true,
you look at the right hand column. You then pick b - say it's also
true - so you move to the second row of the right hand column, and
see that the "outcome" is false.
Note that we have arbitrarily put values of a as
the columns, and b as rows. We might just have well swopped them
around.
What does it mean?
One of the problems with logic is that all-too-often,
it's difficult to see how logic relates to real life.
(Logicians sometimes appear to take great delight in obscuring the issue)!
Throughout the following
tutorial, we'll try not to fall into this trap. Let's give you a practical
example of how the above truth table might relate to real life:
| SCENARIO 1 |

|

|
You're in a darkened passage. You're facing the passage, and there's
a light switch on your left. You turn on the light switch - flash! - the
light goes on. You walk to the end of the passage. There's another
light switch (let's call the first one, Switch a, the new switch, Switch b).
You flip the second switch and - click - the light is off again.
|

|
|
Do you see the analogy? At the start a=0 and b=0 (both switches are
off) and the light (or 'output' if you wish) is also off. When a=1 (you
turn on the first switch), then Out becomes 1 - the light goes on.
Remember that the second switch is still off. Flip the second switch
(b=1) and - click - the light goes off again. (To complete our truth
table, we should actually grope our way back down the darkened passage
and flip the first switch again to check that with a=0 and b=1, the
light goes on again)!
If your browser understands JavaScript, you can actually
try this out by clicking with your mouse on the 'switches' above!
Note the symmetry - both could have been in the "on" position.
Fancy Names
There are fancy names for all the sixteen possible truth tables that we
could get out of our black box. It won't surprise you to learn that several of
the options have more than one name - humans are like this.
Fortunately, you will commonly encounter only a handful of the sixteen.
The one we made above (Known as Exclusive Or or 'XOR' to its friends)
is not quite as familiar as the others, which is why we perversely
chose to explore it first! Here are four common ones:
|
AND a b
|
Value of a
|
| False
| True
|
| Value of b |
False
| 0
| 0
|
| True
| 0
| 1
|
|
|
OR a b
|
Value of a
|
| False
| True
|
| Value of b |
False
| 0
| 1
|
| True
| 1
| 1
|
|
|
IMPLIES a b
|
Value of a
|
| False
| True
|
| Value of b |
False
| 1
| 0
|
| True
| 1
| 1
|
|
|
EQUIVALENT a b
|
Value of a
|
| False
| True
|
| Value of b |
False
| 1
| 0
|
| True
| 0
| 1
|
|
More meaning
Continuing our irritating habit of trying to make these tables meaningful,
Can you relate any one of the above to real life?
Yep. All of them are relevant to real people like you (and, we hope, me).
-
AND is commonsense. If we say something like "Sting AND Mandela were
there", then the statement is palpably false if one of the two, or
both, didn't show up. It's only true if BOTH Sting AND Mandela pitched.
- OR might be a bit more tricky, if we didn't understand that here "OR"
means "EITHER a OR b , or indeed, BOTH". A statment of "OR" fails only
if both components turn out false. Either one will suffice to make the
statement true.
- IMPLIES is trouble. A 'better' (but synonymous) way of reading
"IMPLIES a b " is to say:
for example, "If it rains THEN I'll bring an umbrella". Clearly, this
only fails IF it rains AND I DON'T bring that dratted umbrella. If it's
sunny, ie a is FALSE, then who cares?
Thank Ronald de Sousa for the umbrella
analogy.
- EQUIVALENT is not difficult. The conclusion we make from the
truth table is that EQUIVALENT is true if the items are the same (both
true or both false) and otherwise, it is FALSE. Makes sense, doesn't it?
Learning to say 'Not'
Look at the two truth tables for XOR and EQUIVALENT:
|
EQUIVALENT a b
|
Value of a
|
| False
| True
|
| Value of b |
False
| 1
| 0
|
| True
| 0
| 1
|
|
|
XOR a b
|
Value of a
|
| False
| True
|
| Value of b |
False
| 0
| 1
|
| True
| 1
| 0
|
|
Can you see
that if we "changed 0's to ones, and 1's to zeroes", we could transform
the one table into the other? We have a fancy way of "turning around
zeroes and ones" - the magic word is NOT. The more you think about
it, the more it makes sense. NOT EQUIVALENT does seem to imply the same
sort of logical step as "XOR". What about NOT AND? Here it is:
|
NAND a b
|
Value of a
|
| False
| True
|
| Value of b |
False
| 1
| 1
|
| True
| 1
| 0
|
|
You can see that with "NAND" (NOT AND), a statement is always true
unless both inputs are true.
NOT only can one apply such logic to any of the sixteen possible
truth tables, you can even apply NOT to a single bit. So NOT(0) is
1, and vice versa!
Getting even more sneaky
We know that the result of a statment, for example "XOR a b ", will be either
true or false (1 or 0, if you prefer). The result of another statement
will likewise be either one or zero. Can we combine these two "results"
using our "fancy truth-table operations"? Can we, for example, say
AND ( (AND c d) (AND a b ) ) ?
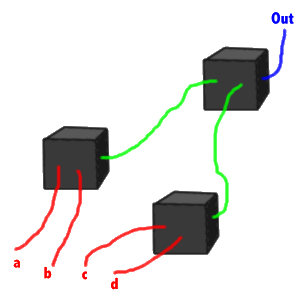
There's no reason why we shouldn't!
It's just the same as taking several black boxes, and connecting the
outputs of some to the inputs of others:
Once we start doing this, all sorts of fun things happen. We can derive
rules about what happens when we combine certain "truth table
operations". But before we start doing so, let's think up a more snappy
name for "truth table operations". Hmm, how about "binary operators?"
No, not enough zip and zing, and "NOT" isn't binary. "Logical operators?"
- hmm, hardly. That's the problem with logic, every synonym is worse than
the next. (Some even use the term "logical connectives")!
Here's an indigestible table that shows just how confused people
are when it comes to naming things in logic. Are you ready?
| Our term:
| AND
| OR
| IMPLIES
| EQUIVALENT
| XOR
| NOT
|
| Synonyms
| &


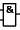
|
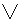
/
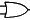
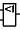
| =>
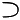
'if..then'
| <=>
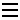
'biconditional'
|
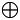
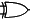
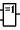
| ~
'
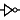
"inverter"
|
The above becomes less confusing when one realises that people talk
about the same things in different contexts. We might say IF..THEN,
a computer circuit designer might have a set of logic gates (a black box,
if you wish)doing the same thing, and a logician might write a formula using the
shorthand "=>". So it's probably worthwhile knowing several versions
of the same "operator".
Things get even worse, and we haven't even talked
about set theory! The fancy name for "&" is
an ampersand; for "/" a slash, oblique stroke, solidus, or virgule; for "~" a tilde,
for "^" a caret, and so on. In some computer languages, "^" is used to
express "exclusive or".
Some use "+" for OR, and "*" for AND.
Also note the little o
to the right of the triangle in the electronic symbol for a NOT gate.
This is often placed on its own (without the triangle) on the input
or output lines of another gate (eg an AND gate) to signal that the
input or output has been inverted.
Rules
Think about how we said above that "NOT EQUIVALENT is the same as XOR".
Could we translate (!) this English statement into a combination of our
by-now-familiar symbols? Of course! Here's the translation:
NOT ( a EQUIVALENT b ) EQUIVALENT ( a XOR b)
Another way of saying this is:
~ ( a <=> b ) <=> ( a  b)
b)
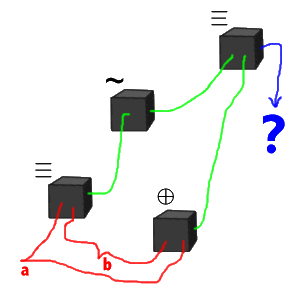
This looks well and good, but is there some way of proving
the above assertion? Yes, in fact there are several. Think about our
little black boxes, connected together. We might conjure up
something like:
Look at the above mess of wires and boxes. On the left we have
a and b feeding into a box that does an "implies". On
the right, the same inputs feed into an "xor". The output of the first
box is then inverted by a "not" box, and feeds into the distant "implies"
box together with the result of the xor.
you can see that if the final result (on the line that's coloured blue)
is always TRUE, then we know that our assertion is valid. In other words,
we would have proved that:
~ ( a <=> b ) <=> ( a  b)
b)
Okay, we now have a good idea of what we're talking about, but we
are no closer to proving this assertion. One way we could obtain proof
is simply using truth tables. We can create a humungous truth table
thus:
| Option
| a
| b
| a <=> b
| a 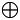 b b
| ~ (a <=> b)
| ~ (a <=> b) <=> (a 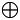 b) b)
|
| (1)
| 0
| 0
| 1
| 0
| 0
| 1
|
| (2)
| 0
| 1
| 0
| 1
| 1
| 1
|
| (3)
| 1
| 0
| 0
| 1
| 1
| 1
|
| (4)
| 1
| 1
| 1
| 0
| 0
| 1
|
You can see what we've done. We only have four ways we can combine
a and b - Options (1) to (4). For each of these combinations,
we look up the intermediate steps (using the truth tables for
EQUIVALENT and XOR), and finally we work out that
~ ( a <=> b ) <=> ( a 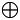 b) is
always TRUE. So we've proved the formula is a "valid proposition"
- it is always true.
b) is
always TRUE. So we've proved the formula is a "valid proposition"
- it is always true.
Here's where the logicians get in on the act. Consider a
statement like:
~ p
the result of which obviously depends on the value of p.
Logicians will say that this statement is "contingent",
(which is another way of saying "it depends"),
while our formula:
~ ( a <=> b ) <=> ( a 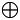 b)
b)
is a "valid proposition in the propositional calculus
with arguments a and b".
We explore the propositional calculus in detail in a moment, but first,
a note on nonsense..
Nonsense
It should also be evident that not all the combinations of symbols
we can write down make sense. For example, what of:
p ~
.. which doesn't seem to make any sense at all. There must be rules
for constructing "well formed formulas". There are. They make use of
the properties of the binary functions we have already described:
AND, OR, IMPLIES and EQUIVALENT, as well as the unary function NOT.
(Most people don't bother about XOR).
In order to examine the rules, we need to make up "place holders" that
allow us to break down a formula. For example, if we have
((x AND ~y) OR (~x AND y)) AND (z OR w)
You can see this of the general form "a AND b":
|
((x AND ~y) OR (~x AND y)) | AND | (z OR w) |
| |
|
| a | AND | b |
To distinguish between
variables (such as x, y,z and w), and "place holders" (which might stand
for a whole lot of different symbols), we could use
Greek 'letters' such as alpha, beta, gamma and so on, instead of the
clumsy term "place holder", or even worse, totally confusing ourselves by
using the same symbols such as a and b for both variables
and place holders. This approach should allow us to
progressively break up all formulae into recognizable patterns.
For example, we can now less ambiguously render the above:
|
((x AND ~y) OR (~x AND y)) | AND | (z OR w) |
| |
|
| alpha | AND | beta |
and then proceed to further break things down into:
|
( | (x AND ~y) | OR | (~x AND y) | ) | AND | (z OR w) |
| |
| |
|
| ( | gamma | OR | delta | ) | AND | beta |
| |
|
| alpha | AND | beta |
.. and so on.
Note that logicians again get in on the act. Because our "place holders"
are not actually variables, but things that "talk about the structure of
our logical system", they are called metalogical variables. Generally,
when a logician (a) wants to confuse you and (b) wants to talk about
something in a 'system of equations' (or whatever), but from outside
that system, he will somewhere prepend the two little syllables meta.
With this under our belt, let's look at the rules for our system.
(We will abbreviate the term "well-formed formula" to WFF).
|
Rule 3: Well-formed Formulas |
Given the metalogical variables alpha and beta:
- If alpha is a WFF, then "~ alpha" is too;
- If alpha and beta are WFFs, then "alpha & beta" is also a WFF, and likewise for:
- "alpha v beta"
- "alpha => beta", and
- "alpha <=> beta"
|
Note that we commonly use 'brackets' (parentheses) to group logically
terms, as we did in our example: "((x AND ~y) OR (~x AND y)) AND (z OR w)".
We will generally use brackets, although we could define "rules of precedence"
so that, for example, not takes the highest precedence, AND comes next,
and OR has a servile status, (but parentheses are better)!
We end up demonstrating that our example is actually a WFF,
simply by progressively breaking down the whole complex formula
into 'chunks', each of which is itself a WFF.
There is a more formal way of representing
what we just said. It's called..
Backus Naur Form
.. which is otherwise variously known as "BNF" or even "Backus Normal Form"
(Poor old Peter Naur often gets left out of the picture, mainly because nobody can
remember his name, but also because he was 'only' the editor of John W Backus'
original report describing the programming language ALGOL)!
BNF is simply a powerful way of representing structure.
BNF is made up of "terminals" (which are simply letters such as A, b, X, Z, y
and so on, or characters such as ".", "," et cetera) and the more interesting "non-terminals" which are simply
metalogical variables - that is, made up of terminals and/or other
metalogical variables. In BNF we represent metalogical variables rather
strangely, thus:
<I_am_a_metalogical_variable>
in other words, the name of the metalogical variable (non-terminal) is encased in <angle brackets>
We have a few other strange conventions. When we define a non-terminal,
we do so by putting it's name on the left, follow this by " ::=", and
then follow this with the actual definition. Definitions are powerful.
Look what we can do. We can:
- Use pipes ("|") to select from one of several options:
<something> ::= <option1> | <option2> | <option3>
- Join several things together ("concatenate" them) by just
plonking them side by side:
<something2> ::= <first_thing><second_thing>
- Select from a range of terminals:
<alphabeta> ::= A..Z
As an example, what does the following define?
<floating_point_number> ::= <mantissa><exponent_part>
<exponent_part> ::= E<signed_integer> | NULL
<mantissa> ::= <signed_integer> | <signed_integer>.<afterwards>
<signed_integer> ::= -<before> | +<before> | <before>
<before> ::= 0 | <nonzero><afterwards>
<afterwards> ::= <digit> | NULL | <digit><afterwards>
<digit> ::= 0 | <nonzero>
<nonzero> ::= 1..9
Clearly, a clumsy attempt to define the format of a floating-point number,
something along the lines of, for example, 3.14E-99 or 0.1900 or whatever.
If you more than glanced at the above, you should have several questions
and observations burning in your mind. Here they are:
- BNF allows recursion - in other words, a non-terminal
can refer to itself, and so on (even to infinity)!
- concatenation and pipes can be combined in the same definition;
- There's something very special called NULL.
- Characters such as "+", "-" and "." are treated just like any
other terminal.
You can work out what NULL means. It means "put in absolutely nothing",
and is obviously extremely useful. Try writing the above without it. You
can, but it's tedious! Also note that BNF as rendered above is far from
perfect. You might ask yourself how you render "|" pipe characters
themselves in BNF, how to represent a space, and how to represent a
greater than or less than sign!
Also note that
some people use an arrow pointing to the right, instead of "::="
Returning to our friend the WFF, consider:
<WFF>::= p | q |
~ <WFF> |
<WFF> v <WFF> |
<WFF> & <WFF>|
<WFF> => <WFF> |
<WFF> <=> <WFF>
.. which would pretty well say in a single line what we said
above with five rules! Note that here we have limited our terminals to
"p" and "q", but we can easily extend our BNF to encompass more terminals.
We could say:
<WFF>::= <termin>|~<WFF>|<WFF>v<WFF>|<WFF>&<WFF>|<WFF>=><WFF>|<WFF><=><WFF>
<termin>::= a .. z
See how, owing to inherent laziness, we've replaced all the letters
from a .. z (oops, I did it again), with ellipsis. (That's what
we call the double dots).
Note that there's nothing magical about BNF. All it does is give us
a convenient way of representing syntax - a description of how
things are put together.
Recursion
As a brief aside, did you see how we used the term <WFF> within
the definition of a WFF? This is another example of recursion.
Powerful indeed, but beware - it can go on forever. For example, if we take our definition again:
<WFF>::= <termin>|~<WFF>|<WFF>v<WFF>|<WFF>&<WFF>|<WFF>=><WFF>|<WFF><=><WFF>
We note that we could create the WFF:
~ p
but also the formula:
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ p
and so on (ad infinitum)! Recursion can bite.
A Context-Free Grammar (CFG)
Here we come across another intimidating TLA (three letter acronym) -
the CFG. But you understand what a CFG is already. It's a collection of:
- An 'alphabet' of terminals;
- A set of nonterminals;
- A set of rules of the form:
<nonterminal> ::= a string that's a mix of terminals and/or nonterminals
Note how we've constructed a metalanguage - a language that
talks about the structure of a language. We have a fancy name for the
"language generated by the CFG" - we call it a context-free language!
You wouldn't be wrong if you guessed that "context-free language" is
often abbreviated to CFL !
We've perhaps been a bit vague in saying: "a string that's a mix of terminals and/or nonterminals".
We'll leave you to construct a "meta-metalanguage" that (a) defines the
way you can create a nonterminal, and (b) gives you a headache!
BNF and Internet Savvy
It's common to represent BNF using <angle brackets>. This is not
only a clumsy read, but if you're creating a web-page, angle brackets
are used for other things. They are also a pain to type. How about the following
convention?
- All terminals are typed as is;
- All non-terminals are underlined!
Let's do this for our example above:
floating_point_number ::= mantissa exponent
exponent ::= E signed_integer | NULL
mantissa ::= signed_integer | signed_integer.afterwards
signed_integer ::= - before | + before | before
before ::= 0 | nonzero afterwards
afterwards ::= digit | NULL | digit afterwards
digit ::= 0 | nonzero
nonzero ::= 1..9
The added advantage is that in hypertext, we can implement any
nonterminal on the right of an equation as a hyperlink!
The Propositional Calculus
We're now ready to define the propositional calculus a little more
formally than above. Here goes:
The Propositional Calculus can be defined as a context-free
grammar, with:
- An alphabet of terminals:
terminal ::= a | b | .. | z
- The set of the following nonterminals, and the rules of their construction:
We have now defined the syntax of the propositional calculus, but
what about it meaning (what logicians call "semantics")? Now that we have
the structure, the semantics become clear. For we already know that we
can substitute 1 or 0 for the "variables" a .. z, and we also know the
meanings of the various operations - for we've looked at their truth
tables in detail!
You can see that (especially as we've introduced brackets into our
syntax) not only can you check the validity of a formula in the calculus,
you can also easily substitute in values for variables, use our truth tables to
combine these, and come up with a result - either true or false! And this
is all we're interested in isn't it - our Rule one?
Other than making a great big truth table, we still don't have a formal way of proving a formula
in the PC. Is a statement in the PC a "valid proposition" or is it
contingent, or is it in fact always false? Clearly, if we have a large
formula, we don't want to sit down and examine every possible case -
we want to know whether a formula is valid or not. Is there a way of
doing this? Fortunately, there is. It's called..
Wang's Algorithm
Wang's algorithm is a mechanistic approach to deciding whether an
assertion in the propositional calculus is true (or undecidable).
It involves less computation than mucking around with truth tables.
Hao Wang published this really rather smart approach in about 1960.
His coding whipped through about 350 theorems from Bertrand Russell's
Principia Mathematica, proving them all.
The idea is that we are given certain statements (premises), and a theorem
we wish to prove. Here's the mechanism of proof:
|
"Rule" 4 - Wang's algorithm |
- Write the premises separated by commas, followed by an arrow
(
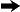 ), and then the theorem to prove.
), and then the theorem to prove.
- if a formula is negated, remove the "~" and move the formula
to the opposite side of the arrow;
- if any formula on the LEFT has the format "(alpha & beta)",
replace this with "alpha, beta"; similarly, any formula on the RIGHT
with format
(alpha v beta) can
be replaced with "alpha, beta".
- any formula "(alpha v beta)" on
the LEFT must be turned into TWO lines, one containing alpha, and
the other, beta. Both lines must be proved. Likewise for AND
on the right!
- If at ANY point the same formula appears on both sides of an arrow,
that line is PROVED (succeeds);
- If none of: v, & or ~ is
left anywhere in a line, and condition (5) hasn't been met,
then the line cannot be proved - the theorem is INVALID.
|
Note that Wang's algorithm talks only about AND, OR and NOT. What about
IMPLIES, EQUIVALENT, and such exotica as XOR? The answer is that you have
to convert these "logical connectives" to AND, OR and NOT. Yes,
you can convert, but before we explore such conversion in detail,
let's try an example. We'll use one stolen from
Chris Mellish:
"If the Russians get ahead of the Americans in the arms race, they will
take over the world. If the Russians announce that they are cutting their
arms budget, Congress will cut the American arms budget. If the
Americans cut their arms budget, but the Russians do not cut theirs, the
Russians will get ahead of the Americans in the arms race. The Russians
are devious and will announce that they have cut their arms budget
in any case. Either the SALT talks will fail or the Russians will cut
their arms budget.
If the SALT talks fail, will the Russians take over the world?
If the SALT talks don't fail, will the Russians take over the world?"
How can we approach this? Well, here are our variables:
a: "Russians get ahead of the Americans in the arms race"
b: "Russians announce they are cutting their arms budget"
c: "Americans cut their arms budget"
d: "Russians cut their arms budget"
e: "SALT fails"
f: "Russians take over the world"
And here are the premises we get from Mellish's text:
P1: a => f
P2: b => c
P3: c & ~ d => a
P4: b {in other words, b is TRUE}
P5: e 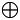 d
d
And our theorems we wish to prove..
T1: e => f
T2: ~e => f
You can see that we first need to represent statements such as
a => f
and
e 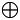 d
d
in terms of NOT, AND and OR. How might we do this?
Play around a bit, and try and do just this for "IMPLIES"! You might come up
with something along the lines of:
(a => f) <=> (f v ~ a)
In other words, saying "a implies b" is the same as saying "b OR NOT a".
Verify this using a truth table, as we did for XOR and NOT EQUIVALENT, above.
Next, try and find an equivalent expression for XOR, using only NOT, OR and AND.
You might get:
e 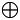 d <=> (e v d) & ~ (e & d)
d <=> (e v d) & ~ (e & d)
What we are saying is that "e XOR d" is the same as "(e OR d) AND NOT (e AND d)".
(Can you think of a better way of saying the same thing?). You can think up
a 'constructive proof' that the one formula can be substituted for the other -
consider a black box that, for example, does an "e XOR d". Clearly, if we
clip this box out and plug in another box that does exactly the same thing
to its inputs, what goes on in the box - (e OR d) AND NOT (e AND d) - doesn't
matter in the slightest.
Armed with these equivalence transformations (that is, expressions that
we can substitute for e.g. XOR and IMPLIES), we can reformulate our premises:
P1: f v ~ a
P2: c v ~ b
P3: a v ~ (c & ~ d)
P4: b
P5: (e v d) & ~ (e & d)
And our theorems..
T1: f v ~e
T2: f v ~(~e)
Let's now apply Wang's algorithm to T1. We will tick all lines that
succeed (and then allow them to disappear). In the ticked lines, the
identical formulae will be shown in red. Here
goes..
| Step
| Statement
| Justification
|
| 1
|
P1,P2,P3,P4,P5
 T1
T1
| Wang 1
|
| 2
| f v ~ a, c v ~ b, a v ~ (c & ~ d), b, (e v d) & ~ (e & d)
 f v ~ e
f v ~ e
| Substitution
|
| 3
| f v ~ a, c v ~ b, a v ~ (c & ~ d), b, e v d, ~ (e & d)
 f, ~ e
f, ~ e
| Wang 3
|
| 4
| f v ~ a, c v ~ b, a v ~ (c & ~ d), b, e v d, e
 f, e & d
f, e & d
| Wang 2
|
| 5
|
f v ~ a, c v ~ b, a v ~ (c & ~ d), b, e v d, e
 f, e
f, e 
f v ~ a, c v ~ b, a v ~ (c & ~ d), b, e v d, e
 f, d
f, d
| Wang 4
|
| 6
|
f , c v ~ b, a v ~ (c & ~ d), b, e v d, e
 f, d
f, d 
c v ~ b, a v ~ (c & ~ d), b, e v d, e
 f, d, a
f, d, a
| Wang 4, 2
|
| 7
|
c v ~ b, a v ~ (c & ~ d), b, e , e
 f, d, a
f, d, a
c v ~ b, a v ~ (c & ~ d), b, d, e
 f, d, a
f, d, a 
| Wang 4
|
| 8
|
c v ~ b, a, b, e
 f, d, a
f, d, a 
c v ~ b, b, e
 f, d, a, c & ~ d
f, d, a, c & ~ d
| Wang 4, 2
|
| 9
|
c, b, e
 f, d, a, c & ~ d
f, d, a, c & ~ d
b, e
 f, d, a, c & ~ d, b
f, d, a, c & ~ d, b 
| Wang 4, 2
|
| 10
|
c, b, e
 f, d, a, c
f, d, a, c
c, b, e, d
 f, d, a
f, d, a
| Wang 4, 2
|
|
|
|
|
(We come to the paranoid conclusion that one would expect, given
the nature of the original premises, which were presumably constructed
in the good old USA in about the fifties)!
We leave T2 for your entertainment.
For a LISP rendition of Wang's algorithm (after
Tanimoto), see Lee Spector's page
Equivalence Transformations and Unnecessary Fussing
Considering the elegance of Wang's algorithm (and it's relative ease
of implementation on a computer) it's rather sad that many people
have spent considerable time working out other complex ways to
solve theorems in the propositional calculus (PC). We have seen how with
the bare minimum of equivalence transformations, Wang's algorithm
whips through theorems. You will however encounter zillions of
theorems in the PC, often with associated eponyms, obfuscation,
and even mystique! Here are a few examples:
Modus ponens: P => Q, P therefore Q
Modus tollens: P => Q, ~Q, therefore ~P
Hypothetical Syllogism: P => Q, Q => R, therefore P => R {also called "transitivity of implication"}
Disjunctive Syllogism: P v Q, ~ P, therefore Q
Simplification(1): P & Q, therefore P
Simplification(2): P & Q, therefore Q
Introduction (importation): P, Q therefore P & Q
Constructive Dilemma: P v Q, P => R, Q => R, therefore R
Law of excluded middle: P v ~P
RULES OF REPLACEMENT
De Morgan(1): ~ (P & Q) can be replaced by ( ~ P v ~ Q)
De Morgan(2): ~ (P v Q) can be replaced by ( ~ P & ~ Q)
Commutation(1): (P & Q) can be replaced by (Q & P)
Commutation(2): (P v Q) can be replaced by (Q v P)
Association(1): (P & (Q & R)) can be replaced by ((P & Q) & R)
Association(2): (P v (Q v R)) can be replaced by ((P v Q) v R)
Distribution(1): (P & (Q v R)) can be replaced by ((P & Q) v (P & R))
Distribution(2): (P v (Q & R)) can be replaced by ((P v Q) & (P v R))
Double negation: ~ ~ P can be replaced by P
Contraposition ("transposition"): P => Q can be replaced by ~ Q => ~ P
FALLACIES (incorrect)!
Affirming the Consequent: P => Q, Q, therefore [wrong!] P
Denying the Antecedent: P => Q, ~ P, therefore [wrong!] ~Q
Note that in all of the above, we were wicked. Instead of
using P, Q, and R, we should really have used alpha, beta and gamma,
as we're actually talking about metalogical variables. Tsk, tsk.
A bare minimum
Seeing that we can make XOR, IMPLIES and so on with just OR, AND and NOT,
you may well have asked yourself "How many 'logical connectives'
do we need as a minimum to do anything in the PC?"
Surprisingly, the answer is "Just One"! The trick is, you must choose
carefully. Try creating other 'connectives' using just NAND.
You'll find that it's a cinch.
Some confuse you by referring to NAND as a "complete base"
because you can use it to make all the others.
AND and NOT together likewise make up a complete base.
More
We still need to talk about Push-down automata, Turing Machines, and
Regular expressions. Later we might also explore digital circuitry in
detail. We also need to tell you about Church and Gödel. We might
even look at the Predicate calculus, and set theory. So much to do!
Index/Glossary
References
Books
You can do no better than look at:
- Cohen Daniel IA: Introduction to Computer Theory. Wiley, 1986.
A superb book.
- Feynman Richard P: Feynman lectures on computation. Penguin 1999.
Perhaps the greatest mind of the 20th century; certainly an inspired teacher.
Explores all sorts of things, brilliantly.
Web References
A few bits and pieces: