Elastic Properties of the Chest Wall
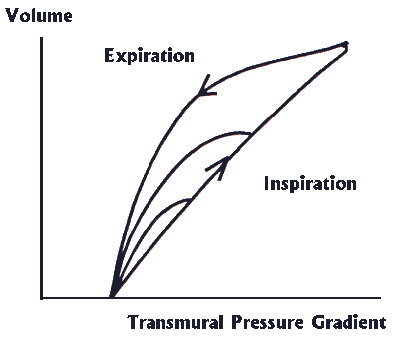
It is vital to distinguish between the elastic properties of the
lung and those of the surrounding chest wall. All too often, clinicians
(especially those in ICU) confuse total thoracic compliance with
lung compliance. When we come to discuss acute lung injury, we will
see that it is the pressure distending the alveolus that is critical
in determining whether we injure the lung with our ventilation.
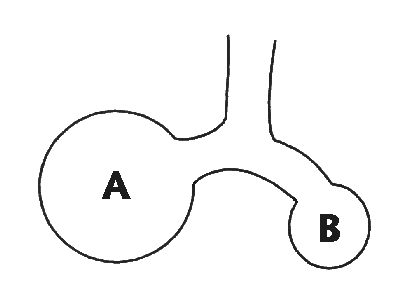
If we were to take a rabbit (for example), encase its chest wall
in plaster of Paris, and then ventilate it using high transthoracic
pressures, we would not necessarily be inflicting high transpulmonary
pressures on the unfortunate animal. We know from the few studies that
have looked at this, in the critically ill, that total thoracic
compliance often bears little relationship to pulmonary compliance!
How do we separate pulmonary and chest wall compliance?
In order to do this, we need some measure of intrapleural pressure,
that is, the pressure within the "potential" space between the pleura.
Unfortunately, this is not easy to obtain, and the pressure also varies
with the site of the transducer and the posture of the subject. The
easiest method of obtaining a measure of this pressure is to use an
intra-oesophageal balloon catheter, as a correctly positioned oesophageal
balloon reflects intra-pleural pressure with 'reasonable' fidelity.
Air-filled balloon catheters are commonly used for this purpose.
A noteworthy point is that if the thoracic cage is opened,
the lungs tend to collapse, but the thoracic cage will tend to
expand to a volume about one litre greater than FRC (in an adult).
Interestingly, the diaphragm too contributes to this complex
relationship, as even when relaxed it has a residual tone that
enhances the functional residual capacity of the lung by about
400ml. (This tone is abolished during anaesthesia)!
Note the relationship between total thoracic compliance,
lung compliance, and chest-wall compliance:
1 / Ctotal = 1 / Clung
+ 1 / Cthoracic cage
Some people use the idea of elastance where the elastance
is the reciprocal of the compliance. We can then add elastances,
rather than adding the reciprocals of compliances. It seems terribly
wanton to introduce new terms, for the inability to take a reciprocal!
Regional Variation in Lung Ventilation
Ventilation within the lungs is greatest near the bases, in the
upright position. This is probably mainly due to variation in intra-pleural
pressure as we move from apex to base - pressure is more negative near the
apex. Effectively, this probably causes more expansion of the apices at
FRC. As the person inhales, it is easier to expand the bases, as these
are less distended than the apices! Note that at lower lung volumes, the
situation may be reversed, with poor ventilation of the bases.
Lung Volumes
Clinicians especially, lay great emphasis on lung volume, its subdivisions,
and divergence of volumes from normal. This is peculiar, as there is
relatively little evidence that changes in volume, even quite gross
derangements, are consistent predictors of clinical outcome in the
individual patient, especially post-operatively. Physiologists (who are
often "splitters" at heart) have labelled a variety of components of the total
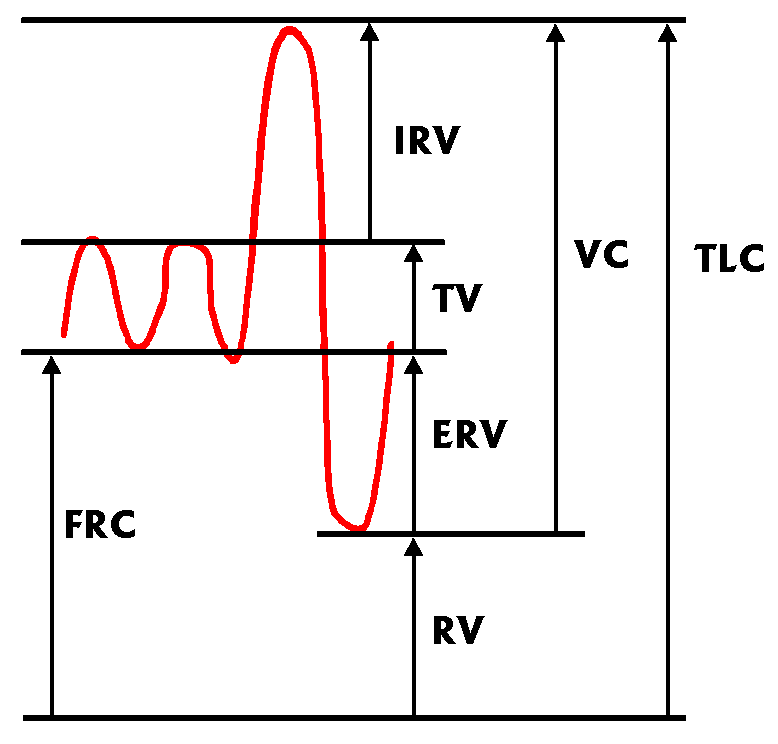
lung capacity. The following diagram shows the changes in volume (on the
vertical axis) against time (on the horizontal axis) as an individual
breathes, initially tidal volumes, and then inspires and expires maximally.
are:
- FRC = Functional Residual Capacity
- TV = Tidal Volume
- VC = Vital Capacity
- RV = Residual Volume
- TLC = Total Lung Capacity
- ERV = Expiratory Reserve Volume
- IRV = Inspiratory Reserve Volume
Note that simple spirometry obviously cannot provide any of the volumes
that include RV, the residual volume left in the lung after maximal
expiration. We need other methods to find TLC and FRC.
Perhaps the volume that has received most attention is the Functional
Residual Capacity (FRC), the volume of gas in the lung after a normal
expiration. The FRC is determined by the balance between
the inward elastic recoil of the lungs, and the outward recoil of
the thoracic cage, mentioned above. As already noted, the FRC decreases
with paralysis and anaesthesia. Other factors influencing the FRC
include:
- Body size (increase of about 32-51 ml/cm of height)
- Gender (10% less in women of the same height)
- Posture (Supine posture decreases FRC by 0.5 to 1 litre
in an adult)
- Lung pathology.
Note that there is no substantial effect of age on FRC!
Measuring FRC
There are Three main approaches to measuring FRC:
- Nitrogen washout
The subject breathes 100% O2, after breathing
air. If we collect all the expired gas, and measure the
final concentration of nitrogen in the pooled expired gas
we can calculate the volume present in the lung at
the start of the washout. Knowing the concentration
of N2 in air (78%) we can calculate FRC.
- Helium wash-in
The subject is connected to a spirometer of known volume,
containing a known amount of helium. After
equilibration, the new concentration of helium is noted,
and used to determine total volume. We know the concentration
of helium before (C1) and after (C2), we know the spirometer volume
(V1) and can therefore determine the FRC using:
V2 = V1 * (C1 - C2)/C2.
- Body plethysmography
The subject is placed in a "body box", which is gas-tight.
(S)he breathes against an occluded airway, and pressure
changes at the mouth and in the box are recorded. Application of
Boyle's law then permits calculation
of FRC:
- We find the change in box volume,
 V by:
V by:
P1.V1 = P2.V2 (by Boyle's law) and
V2 = V1- V, thus
V, thus
P1.V1 = P2.
(V1 - V)
V)
- Next we apply Boyle's law to the gas in the lung,
where
P3V3 = P4.(V3 +  V),
V),
and knowing P3, P4 and  V,
we can therefore determine V3, the FRC.
V,
we can therefore determine V3, the FRC.
Dead Space
Not all the air that passes into the respiratory tract reaches alveoli.
Even in normal individuals, about one third of a tidal volume is wasted
in the anatomical dead space! (This is a remarkably constant proportion
for most animals, even giraffes!) We often talk about the
VD/VT ratio, in other words, the ratio of dead
space to tidal volume. Dead space may be:
- Apparatus dead space
- Anatomical dead space (related to the volume of the
conducting passages)
- Alveolar dead space (related to alveoli that are well
ventilated but poorly perfused, so they effectively contribute
to the dead space).
The physiological dead space is the sum of the anatomical and alveolar
dead spaces, and represents all components of the tidal volume that
do not take part in gas exchange.
Physiological dead space can be calculated using Bohr's method.
This uses the equation:
[CO2]A * (VT - VD)
= [CO2]expired VT
In other words, the product of alveolar CO2 concentration and the
amount of inspired air reaching the alveoli equals the expired CO2
concentration times the tidal volume. It is easy to measure the
tidal volume and the expired concentration of CO2, so all we need
to determine physiological dead space is the alveolar CO2 concentration.
In most cases, we can simply substitute in the arterial PCO2, as
the two are generally very similar.
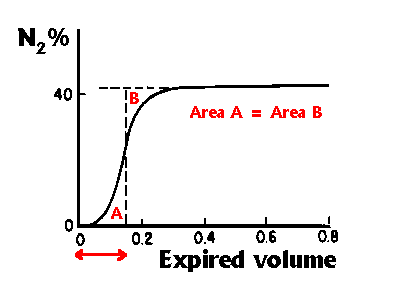
The Anatomical dead space can be determined by watching the
change in N2 concentration (using a rapid N2 analyser) following
a single breath of 100% oxygen. N2 concentration is measured as
the subject breathes out, increasing from zero (at the start of
inspiration) to a plateau (where almost pure alveolar gas is being
expired). Fowler showed that if a vertical line is drawn such that
areas A and B are equal in the following diagram (after West), then
the anatomical dead space is the volume expired up to the vertical
line, indicated by the (red) arrow in the diagram.
The blood:air interface
Movement of molecules across the interface
Gas molecules move with remarkable ease between alveolar air and blood,
traversing the 0.5 micron barrier by passive diffusion. This means that
we can apply all those eponymous little rules which make pulmonary
medicine so irritating - Fick's law, which tells us
that more diffusion will occur if we increase the surface area, decrease
the thickness of the alveolo-capillary membrane, or increase the partial
pressure gradient across the membrane, and also Grahams
law (from which we learn that bigger, or less soluble molecules move more
slowly).
The consequences of these laws are:
- Different gases will have different behaviour: for example,
as nitrous oxide (N2O) diffuses across the alveolar wall
into blood, the partial pressure of (N2O) rises rapidly,
so the main factor determining transport of this gas across the
wall is the flow of blood through the capillaries. In contrast
carbon monoxide is so rapidly and avidly bound by haemoglobin that
the partial pressure across the alveolar wall is always large.
This means that transport of CO is limited by the properties of
the wall, and NOT by capillary flow.
- The main gas we are concerned with is of course oxygen. The
behaviour of O2 lies somewhere in between that of
CO and (N2O). In resting man, the average erythrocyte
spends about 0.75 seconds within the alveolar capillaries, and
is fully oxygenated in about a third of this time. Exercise is
different - here, the erythrocyte may zip through the capillary
in 0.25 seconds, so it is easy to see that if there is any
disturbance in the alveolar wall, oxygen saturation may drop
with exercise. This is the basis for assessing some people with
lung disease (especially restrictive lung disease) by checking
arterial PO2 before and after exercise.
- The behaviour of CO2 is interesting. CO2 diffusion through
tissues is rapid, about twenty times as fast as that of O2, but
it is just conceivable that in severe disease of the alveolar wall
CO2 removal might be limited by diffusion abnormalities.
Things become more complex, for two reasons:
- Oxygen diffusion is also affected by the further distance that
gas molecules have to move before they encounter a haemoglobin molecule
to react with;
- The rate of reaction of O2 with haemoglobin is finite, and
this delays uptake of O2 by the red cell.
In other words, diffusion is also affected by capillary volume within the
lung. Decreases in diffusion with various diseases may therefore also
be due to structural changes in lung capillaries, and not only "thickening
of the alveolo-capillary interface".
( As an aside, normal individuals at high altitude may also
show diffusion-limited O2 transfer across their alveolar walls,
but otherwise this limitation is a manifestation of pulmonary
disease.)
Based on the above, we define the Diffusing capacity of the lung
as
D
Lgas =

V
gas
/

P
gas
For example, the diffusing capacity of the lung for carbon monoxide,
DLCO is the volume of CO transferred
divided by the difference between alveolar and blood partial pressures
of CO. Experimental determination of DLCO
is thus rather easy, as owing to the rapid uptake of CO by haemoglobin,
the PaCO is always negligibly small provided we get the subject to inhale
a low concentration of CO. DLCO then becomes:
D
LCO =

V
CO / P
ACO
Practically, we determine DLCO using the
single breath method where a single breath of CO is taken, and the
rate of disappearance of CO is calculated after the subject has held their
breath for ten seconds. (Derived from initial and final CO concentrations
in the inspired & expired air). Note that this can be combined with
inspiration of helium for VA determination, killing two birds
with one stone!
An unfortunate
metaphor, as the procedure is safe, its main limitation being the
ability of subjects to hold their breath for ten seconds!
An alternative method of determining DLCO
is the steady state method, where a tiny concentration of CO is
inhaled until a steady state concentration is reached, and the rate of
disappearance is then measured for a further short period, along with
the alveolar concentration. This compensates for the inconstant aveolar CO
concentration that we encounter in the single breath method.
Flow of blood through the Lung
The pulmonary circulation is not merely a pint-sized version of the
systemic circulation. Important contrasts between systemic and
pulmonary circulations exist. These are highlighted by considering:
- Pressure differences
- The tissue surrounding the capillaries
- Sites of resistance within the circulation
- Capacitance vessels
- Distribution of flow within the lungs.
Pressure differences
The pulmonary circulation is a remarkably low-pressure system,
arterial pressures running at a mean of about 15mmHg. In keeping with
this, pulmonary vascular resistance is extremely low, and the pulmonary
arteries are thin-walled. The reason why this is so is thought to be
one of efficiency - systemic arteries must carry blood to distant organs
and there is considerable variation in and regulation of flow to those
organs. The lung merely accepts the whole blood volume, whatever!
The tissue surrounding the capillaries
There is very little of this - really just the extremely thin alveolo-
capillary membrane, comprising attenuated pneumocytes and endothelial
cells separated by a minute basement membrane. The capillaries can
therefore easily collapse, especially if intra-alveolar pressure is
raised. The peri-capillary tissue is thought to be under tension from
the surrounding elastic lung parenchyma - it is easy to see how the
transcapillary Starling forces might easily change to favour passage
of fluid into the pulmonary interstitium!
Sites of resistance within the circulation
Pulmonary vascular resistance (PVR) is a convenient fiction, described by
the ratio of pressure change to flow within the circulation. As the
pressure drop within this circulation is normally so small, the PVR
is about one tenth of the systemic vascular resistance. (To confuse
things various units of resistance have been proposed, such as mmHg/l/min,
and dynes.sec.cm-5. Normal values are about 1.8mmHg/l/min, or
140 dynes.sec.cm-5, or perhaps 0.24 kPa l-1min).
This convenient simplification masks vast differences. In the systemic
circulation, the site of resistance is mainly arterial, while in the
pulmonary circulation, there is a substantial contribution from the
capillaries and even from the venous side of the circulation!! This
may have profound implications for assessing the diseased pulmonary
circulation.
Furthermore, as venous or arterial pressure rise, so the
pulmonary vascular resistance falls! This is thought to be
mainly due to recruitment of under-perfused vessels, but may also
be related to distension of capillaries, especially at higher pressures.
Pulmonary volume (that is, amount of air in the lung) also affects
PVR in a complex fashion, PVR being increased at both extremely
low and very high lung volumes!
Capacitance vessels
In the systemic circulation, veins are the main capacitance vessels.
Not so in the lungs, where capillaries distend markedly with pressure
and are important for their capacitive effects.
Distribution of flow within the lungs.
There are remarkable inequalities in blood flow through various regions
of the lung. These variations in flow are mainly related to height above
the heart, which is not too remarkable when one considers the low pressures
present in the pulmonary circulation - hydrostatic pressure alone will
result in a pressure difference of approximately 30cm H20 from the base
of the lung to the apex. This led West to propose his "Three Zones" of
the lung [ West et al. J Appl Physiol 1964 19 p713 ] - in the topmost
Zone 1, there is no flow because the pressure is not sufficient, in
the lowest Zone 3 flow is continuous because intravascular pressure
always exceeds alveolar pressure, while in the middle zone 2, flow
depends remarkably on the difference between arterial and alveolar
pressures - venous pressure is irrelevant as it is lower than alveolar
pressure. Note that in the normal lung, there should be NO zone 1, as
the pressure is just sufficient to perfuse the apices! Some have
subsequenly proposed a "zone 4" which might occur in the bases where
poorly expanded lung might actually result in narrowing of extra-alveolar
vessels with reduced flow.
Of great importance in the lung, especially in disease states, is
hypoxic vasoconstriction. Here, hypoxia in an alveolus causes
marked contraction of that little smooth muscle present in the walls of
nearby arterioles, markedly diminishing flow to the affected region. This
can be seen as an 'attempt' by the lung to normalise ventilation/perfusion
ratios (see below). This vasoconstriction tends to occur dramatically
below a PO2 of about 70mmHg, and may therefore become important at
altitude too.
Ventilation versus Perfusion!
It is clear that adequate lung ventilation and good perfusion are not
enough to ensure that blood passing through the lung is well oxygenated,
and that CO2 is removed. For this gas exchange to take place, there
must be a matching of ventilation and perfusion. Bearing this in mind,
let's take a practical look at causes of hypoxaemia. If the oxygen
content of the blood is diminished despite having normal haemoglobin
levels we have several possible explanations. We therefore take..
A PRACTICAL LOOK AT HYPOXAEMIA
Consider the following possible causes:
- Alveolar hypoventilation
- Shunting of deoxygenated blood past the lung
- Mismatch between ventilation and perfusion: well perfused
- Lowered FiO2
- Diffusion abnormality (in grossly abnormal lungs)
areas may be poorly oxygenated, and vice versa.
We can for practical purposes ignore diffusion in most individuals,
so we are left with four main causes of hypoxaemia. We will here
consider the three most problematical causes: hypoventilation, shunt,
and finally ventilation/perfusion mismatch, often abbreviated to "V/Q
mismatch".
- Alveolar hypoventilation
The
alveolar gas equation in one of its incarnations
(already discussed above) allows us to see the impact
of hypoventilation on oxygenation. It can be seen that
at an FiO2 of 21%, hypoventilation will have
a substantial effect on oxygenation. This is however
easily compensated for by increasing the FiO2. At high FiO2,
even minuscule ventilation can maintain alveolar PO2 for ages.
Note that there may be a lag of several minutes between an alteration
in ventilation and equilibration of PaO2 (and especially, PaCO2). This
is because of the buffering effect of reserves within the body (small
in the case of oxygen, larger for CO2). During this transition period,
values for respiratory quotient will be deranged.
- Shunt
If deoxygenated blood is shunted past the alveoli and not oxygenated,
this will proportionally decrease the oxygen content of the arterial
blood. In normal people, the amount of shunt is tiny (perhaps 1%,
reflecting venous blood from the bronchi entering the pulmonary veins,
as well as coronary venous blood entering the left ventricle via the
Thebesian veins!). Generally, if we cannot determine the amount of
oxygen in the "shunted" blood, we assume that this is the
same as that of mixed venous blood, and make our calculations accordingly.
To calculate shunt, we must know the total amount of blood moving
through the system (QT), and the oxygen content of the arterial, capillary
and mixed venous blood (We will abbreviate these last three to CaO2,
CcO2, and CvO2, the 'standard' abbreviations being a bit more clumsy ).
Knowing these, we calculate as follows:
amount of O2 out = amount in
thus:
QT * CaO2 = Qs * CvO2 + (QT - Qs) * CcO2
Rearranging, we get:
Qs = (QT * CaO2 - QT * CcO2) / (CvO2 - CcO2)
A convenient way of expressing this is to talk of the shunt as a
fraction of QT (We then don't need to know absolute QT). This is
therefore given by rearranging the above to:
Qs/QT = (CcO2 - CaO2)/(CcO2 - CvO2)
It is relatively easy to test for a shunt - simply give the
subject 100% oxygen to breathe, and see if the PaO2 increases. If
there is a true shunt, there will be no response, as the shunted blood
is still not being exposed to the increased FiO2, and so will still
make its evil contribution to arterial hypoxaemia!
- V/Q Mismatch
V/Q mismatch is more tricky than shunt. Theoretically, the ratio of
ventilation to perfusion in any one alveolus can range from zero to
infinity: in the normal individual with a cardiac output of say 5 l/minute
and an alveolar ventilation of perhaps 4l/minute, the ideal ratio would
be 0.8, but even in normal people, there is some variation from this
ratio, most alveolar units falling in the range of 0.5 to 2.0. As one
ages, so the scatter of ratios increases, to perhaps 0.3 to 5.0 ! This
is well shown in Nunn p 167, Fig 8.5.
A convenient method of cheating!
Determining the scatter of V/Q ratios in small sections of the lung is
technically demanding. It is far more convenient (if less accurate) to
regard the lung "as if" it had three compartments comprising:
- well-ventilated poorly perfused alveoli
- well-perfused underventilated alveoli
- optimally perfused AND ventilated alveoli. (The Riley model).
This is clearly sub-optimal, but we can then apply our equations for
shunt and physiological dead space, getting some idea about what is going on. We must
remember that this is only a very poor approximation, however!
Another convenience is to consider the relationship between PO2
and PCO2 within an alveolar unit as we alter the V/Q ratio. Think about
it - if there is no blood flow, then PAO2 might be say 149mmHg (at sea
level), while PCO2 will be zero. With no ventilation, the PCO2 will increase
to that of venous blood (say 45mmHg) with a PO2 equal to the venous PO2,
perhaps 40mmHg. We can therefore plot a curve of PO2 versus PCO2 that
encompasses all possible ratios for alveoli within a particular individual.
Regional variation in V/Q ratios
There are substantial variations in these ratios in the upright lung.
Ventilation increases gradually as we move from apex down to base of the
lung, while perfusion is much more dramatically affected, being low
at the apices and rich at the bases. Thus V/Q ratios decrease as we
move from the apex downwards. This improves with exercise.
Transport
Gas transport to and from the peripery is very elegant. We consider
it briefly:
Oxygen Transport
Most oxygen is carried in the blood as oxyyhaemoglobin.
The small contribution that dissolved oxygen makes to transport is
usually negligible. (It can be calculated using Henry's
law - for each mmHg of PO2 there is 0.003ml O2 dissolved per 100ml
of blood, absolutely minuscule).
Haemoglobin (Hb) is much more effective in transporting oxygen, carrying
about 1.39 ml of O2 per gram of pure Hb. We are all aware of the shape
of the Hb:O2 dissociation curve and its importance in tissue oxygen delivery,
as well as how the curve is right-shifted by:
- lower pH
- higher PCO2 (Bohr effect)
- higher temperature
- higher concentrations of 2,3 diphosphoglycerate in the red cell,
usually induced by chronic hypoxia.
The most convenient equation relating Hb saturation and PO2 is
SO2 = 100 * (PO23 + 2.667*PO2) / (PO23 + 2.667*PO2 + 55.47)
It is however only valid above a PO2 of about 4kPa (30mmHg; PO2 values
in the equation are in kilopascals --- 1kPa is about 7.5 mmHg).
Transport of Carbon Dioxide
This is carried in three forms:
- dissolved
- As bicarbonate
- As carbamino compounds, especially carbaminohaemoglobin.
Because CO2 is twenty times more soluble in blood than is oxygen, about
10% of CO2 carriage is by this method, Bicarbonate is formed from
carbonic acid, which in turn is made from H2O and CO2, the latter reaction
being speeded by carbonic anhydrase within the red blood cells. Bicarbonate
floods out of the red cell, and chloride shifts in in a compensatory manner.
Deoxygenation of blood increases its CO2-carrying ability (the Haldane
effect) because the heightened affinity of deoxyhaemoglobin for hydrogen
ions speeds the formation of bicarbonate, and also because reduced Hb
forms carbamino-haemoglobin more readily! About 30% of CO2 is transported
as carbaminoHb. The CO2 dissociation curve is far more linear than the
Hb curve, and does not display the sigmoid allosteric shape of that curve.
The Tissue Level
As we have indicated, the biggest drop in the oxygen cascade is
here at the level of the tissues. The standard textbooks on
respiratory medicine hardly address this vital issue! I will
update this section as I acquire more information - please feel
free to contribute.
Control
Control of breathing in man is immensely complex.
We will conveniently look at three levels in the control of breathing:
- The anterior horn cell
- The brainstem
- Feedback Regulation
The anterior horn cell
The human respiratory system is interesting in its dual use of both the
diaphragm and intercostal muscles for ventilation.
Shneerson [Disorders of Ventilation Blackwell Scientific 1988, ISBN 0 632 01668 X ]
describes the functional anatomy of the muscular components of the respiratory
pump rather well. We will superficially consider the neuromuscular components.
Descending pathways to the anterior horn cells innervating the
muscles of respiration are:
- bulbospinal fibres in the ventrolateral cord (mainly involuntary);
- more dorsal corticospinal fibres;
- a third fairly diffuse group (for cough, and other non-rhythmic events)
How does the respiratory system compensate for changes in load? This
is very efficient, and compensation occurs within one breath! This is
thought to occur because "instructions to shorten" go to both the muscle
fibres and intrafusal fibres in the muscle spindles. Differential
shortening (caused by a large load preventing shortening of normal fibres)
will be picked up and a large feedback signal will result in further
stimulation of the muscle. Note that this is more important in the
intercostal muscles, as spindles are sparsely scattered in the diaphragm.
The brainstem
Formerly everyone except Ramon y Cajal thought that complicated pontine
mechanisms controlled respiration. The neuroanatomist Cajal got it right
in 1909, claiming that respiratory rhythms originate in the medulla!
There are probably two important groups of neurones, a dorsal group
near the tractus solitarius controlling timing of inspiration, and
a more complex ventral group.
The ventral group includes the (expiratory) nucleus retroambigualis, nucleus
ambiguus, nucleus para-ambigualis (inspiratory), and Bötzinger complex.
There are thought to be at least six types of specific neurones in the
medulla that control respiration.
Pontine regulatory mechanisms do exist, and are thought to "fine-tune"
the above. Various other centres influence breathing, especially in
relation to sneezing, swallowing and coughing. There is a wide
variety of other reflexes that affect breathing including:
- Baroreceptor reflexes (carotid sinus, aortic receptors)
- Lung stretch reflexes (inflation reflex, deflation reflex,
Head's paradoxical reflex)
- J-receptor responses (bronchial and pulmonary juxta-capillary receptors)
- Upper respiratory tract reflexes
- Musculoskeletal afferents (during exercise)
Feedback Regulation
Two sets of chemoreceptors regulate breathing:
- Central Chemoreceptors
These are usually by far the most important. They respond
mainly to changes in cerebrospinal fluid pH. As arterial PCO2
rises, so CSF pCO2 will increase, this causing a drop in pH.
Breathing is stimulated, reducing PaCO2, and so on. With
prolonged respiratory acidosis or alkalosis, the response becomes
dulled, possibly related to compensatory normalisation of the
CSF pH by movement of HCO3- ions.
Severe hypoxia may depress central chemoreceptors.
- Peripheral chemoreceptors
Less important in normal man than the central chemoreceptors,
the carotid bodies become stimulated with:
- hypoxaemia
- low arterial pH (whether due to PCO2 or not)
- hypoperfusion
- fever
- certain drugs (Acetyl choline, nicotine..)
These bodies, the metabolically most active tissue in the body,
contain glomus cells which synapse with nerve endings of the
glossopharyngeal nerve, and their stimulation results in
stimulation of respiration. The peripheral response to PCO2
is about one fifth of the central one.
There is a complex interaction between the peripheral and
central responses to hypercapnia and hypoxia. The response to
PCO2 is slower than that to PO2, linear, and varies widely from
person to person. A typical slope for the CO2 response curve
would be about 2 litres/minute/mmHgPCO2. The curve becomes
steeper at lower PaO2's.
If the PCO2 is sufficiently lowered, apnoea may result, despite
a low PaO2. This is termed the "apnoeic threshold", but may not
be present in some individuals. Metabolic acidosis does not change
the slope of the CO2 response curve, but shifts it left.
The relationship between PaO2 and minute ventilation at constant
PCO2 is complex and non-linear, but if we plot saturation
against minute ventilation, we obtain a convenient almost linear
curve down to a saturation of about 70% !The response to hypoxia
is enhanced by hypercarbia, acidosis and exercise. With gross
hypoxia of rapid onset hypocapnia depresses respiration, but
compensation occurs over about six days. After years of chronic
hypoxia, hypoxic drive becomes markedly attenuated.
References
The readily available textbooks are adequate as an introduction to
the physiology and testing of the lung. Consider using:
- West JB Respiratory Physiology - the essentials 4 ed.
Williams & Wilkins, 1990. ISBN 0-683-08942-0.
A good basic textbook, which has the merit of being short and
explicit.
- Nunn JF Nunn's Applied Respiratory Physiology
4 ed. Butterworth-Heinemann 1993. ISBN 0 7506 1336 X.
A superb book, if you have the time. Go get it!