Kleiber Rules!

Have you ever wondered why clinicians (and even some physiologists) relate a number of measurements to body surface area? For example, they talk about cardiac index (cardiac output divided by, yes, body surface area), and urinary protein losses in nephrotic syndrome as 3.5g/1.73m². Why relate these measurements to area? Does this make sense?

What is the basis of Sarrus and Rameaux's argument? At first glance, it seems quite sensible to argue that:

• As we increase the linear dimensions (L) of an organism, so its surface area increases according to L squared, and weight according to L cubed (Think of a sphere of radius r, with area 4pi.r² and volume 4/3pi.r³ and the result of replacing r with 2r). In other words, weight increases more per unit increase in length than does surface area.
• In any organism, energy loss must balance energy gain, so (unless it is to freeze or burst into flame) heat loss (which should be proportional to surface area) must be counterbalanced by appropriate energy production (metabolism).
• Metabolism will then vary with surface area, and not weight.

QED? Not quite. Nature is often more subtle than nineteenth century mathematicians. It is quite clear that small animals do live fast, short, metabolically hectic existences compared to say elephants, but unfortunately for Sarrus and Rameaux the rule isn't what they predict! We are about to dip into the complex world of scaling.

Scaling Basics

• isometric refers to the geometric similarity of bodies - two bodies with the same proportions are isometric.

• The word allometric refers to bodies that are not isometric, but that change with size according to a particular rule. The term used is generally "allometric scaling", a useful internet search term! We explore in detail rules for allometric scaling.

• dimensionless quantities are ratios between measurements that (as their name suggests) don't have dimensions. For example, if the height of something is 1 metre and its width is 2 metres, we could make up a dimensionless quantity (let's call it the H:W ratio) with a value of 0.5 that relates the two. We divide a length by a length, so the result has no dimensions. Similarly, we might relate the inertial and viscous forces in a fluid, and call this "Reynold's number".

• dimensional correctness. Don't trust all the equations you read in books. First, check that they are dimensionally correct. An example:
  Harris and Benedict derived equations predicting heat production in men and women as follows:
  • For men: Q = 66.4730 + 13.7516(w) + 5.0033(h) - 6.75505(y)
  • Women:   Q = 655.0955 + 9.5634(w) + 1.8496(h) - 4.6756(y)
    
    Where Q is heat production in kcal/day, w = weight in kilograms, h = height in centimetres and y = age in years.

  Consider these for a moment (quite apart from the improbable five to seven digit accuracy). The equations might well give an accurate prediction of energy production, but are they dimensionally correct? Of course not. You can't add weight (dimension L³), to height (dimension L) and obtain a sensible quantity. Kleiber macerated these equations in 1932 (also rather amusingly pointing out that by the above equations, a weightless woman has ten times the metabolic rate of a weightless man)! Do we still use them?

• symmorphosis is a fancy word for a simple concept. The concept, formulated by Taylor & Weibel in 1981, is:

  Biological structures are formed so as to meet but not exceed maximum requirements.

  Think about it - your grandfather's old truck from the 1940's can survive a tornado, but your flashy new car dents if you look at it. Motor manufacturers in the '40s overdesigned like crazy, but now a new species of manufacturer has evolved that knows just what it can get away with. Similarly, an organism is unlikely to put energy into making overgrown bones that can resist being stepped on by an elephant unless part of its daily life involves being stepped on by elephants, an unlikely scenario! If your cardiovascular system is never likely to be taxed more than say ten times the demands on it at rest, not only will the system be structured to cope with a maximum load of 10 times baseline, but each and every component in the system will have this same limitation! Likewise, it would be pointless for the lungs to be able to provide say twenty times the resting oxygen usage if the cardiovascular system could only distribute ten times that basal amount.

• scale independent properties refer to things that don't change with size. Muscles generate the same power and tendons have the same strength (per unit cross sectional area) in most organisms studied. Your bone strength (per unit cross sectional area) is the same whether you're an elephant or an elephant shrew. These properties make sense (perhaps 'collagen is collagen', 'muscle is muscle') but there are other more complex scale independent properties that we don't fully understand! Red blood cells (and capillary diameters) are much the same whatever your body size. Several other body characteristics vary little with the weight of the individual.

• physical constraints are things that limit how much an organism can be modified to cope with changes in scaling. For example, as Schmidt-Nielsen has pointed out so well, you and a flea can perform a standing jump to more or less the same height (The flea can jump 20cm high, you can raise you centre of gravity about 40cm jumping from standing. The only reason why you win is because the flea suffers so much air resistance). But because muscles can only contract so fast (a physical constraint associated with the way muscle works) the flea jumps not by simply contracting its muscles, but by compressing a chunk of highly elastic resilin, and then explosively releasing this. At such a small scale, the muscles simply wouldn't contract fast enough to propel the flea upwards - so the flea has found a trick that overcomes the physical constraint.

  Examples of constraints with scaling implications are:

  • Diffusion is hopeless for transporting anything over more than a tiny distance
  • The solubility of oxygen in water is poor
  • Nerve conduction speeds are limited by physical factors (although "higher" organisms have overcome this to a degree by "re-designing" - developing myelin sheaths)
  • Air resistance becomes important as you get smaller
  • Don't forget blood viscosity!
  • For complex reasons, it appears difficult to "design" a heart that beats at more than about 1300 beats per minute.
  • and so on..
  It is intriguing to determine what the physical constraints are on a complex biological system, but it's even more fascinating observing how nature manages to sidestep such obstacles!

Allometric Scaling Equations

M = a . x^k

where M is the body process in question (for example metabolic rate), x is a measure of the size of the organism, and a and k are constants. For example, a large number of measurements suggest that the relationship between metabolic rate (let's call this P_met) and weight (m_b) is:

P_met = 73.3 * m_b^0.75

.. where P is measured in kcal/day and m_b is the weight in kilograms. This equation, first proposed in 1932 by the brilliant animal researcher Max Kleiber has been amply justified, and is good for men, mice and elephants! There is a small amount of uncertainty about the exact exponent (his original equation actually had an exponent of 0.74) but the value is certainly extremely close to 3/4. There are a whole host of other similar relationships, and many of them depend on similar "fractions involving a quarter" for example 3/4 and 1/4. But before we look at these, let's recall that if we take the logarithm of both sides of an equation, our original equation becomes:

log(M) = log(a) + k * log(x)

You can see that this equation (basically y = c + k*z) is the equation of a straight line. What does this tell us? Simply, that if we want to visualise what's going on in one of the above equations, we can plot log(M) against log(x), and we should get a straight line! We can also indulge in other mathematical meddling - draw a regression line through this log-log plot, draw in the 95% confidence intervals, and the slope of the line will be k, and the point where it meets the y axis will be log(a) (that is where log(x)=0, in other words where x=1).

Max Kleiber

A list of allometries

Little change with weight

1. Maximum functional capillary diameter changes little with weight
2. Red cell size bears no relationship to weight
3. Haematocrit is pretty constant at about 0.45
4. Plasma protein concentrations vary little with size or species
5. Mean blood pressure is about 100 mmHg more or less independent of size or species
6. Fractional airway dead space (V_D/V_T) is pretty constant at about a third
7. Body core temperature is weight-independent
8. Maximal tensile strength developed in muscle is scale invariant
9. Maximum rate of muscle contraction appears scale invariant
10. Mean blood velocity has been calculated to be proportional to m_b^-0.07 (not much variation)

Changes in (almost) direct proportion to weight

1. Heart weight (g) = 5.8 * m_b^0.98
2. Lung weight (g) = 11.3 * m_b^0.98
3. Tidal volume (ml) = 7.69 m_b^1.04
4. Vital capacity (ml) = 56.7 m_b^1.03
5. Lung compliance (ml/cmH₂O) = 1.56 m_b^1.04
6. Blood volume (ml) = 65.6 m_b^1.02
7. Muscle mass = 0.40 * m_b^1.00
8. Skeletal mass = 0.0608 * m_b^1.08

Scaling to the quarter power

1. Heart rate (min^-1) = 241 * m_b^-0.25
2. Blood circulation time (seconds) = 17.4 m_b^0.25
3. Respiratory rate (min^-1) = 53.5 m_b^-0.26

Scaling to the three quarter power

1. P_met (kcal/day) = 73.3 * m_b^0.75       (Our old friend Kleiber)
2. V_O2max (ml/s) = 1.94 m_b^0.79
3. Glucose turnover (mg/min) = 5.59 * m_b^0.75
4. In fact, most metabolic parameters vary with the 3/4 power of the weight. The remarkable implications of this are explored below.

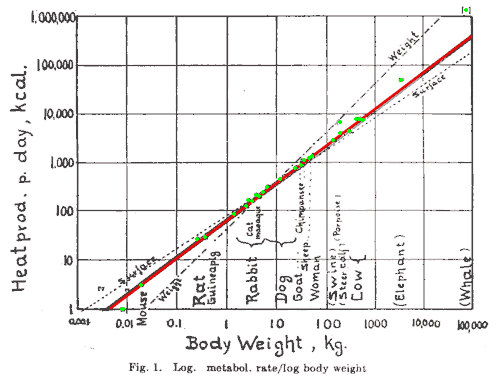
A log-log plot of metabolic heat production against body weight, taken from Kleiber's 1947 article. It is clear that most points (green) closely fit the red line with a slope of three quarters, rather than the weight line (slope of 1) or the surface line (slope of two thirds). Note that although the differences between the lines seem small, this is a log-log plot so the deviations are actually vast! Do you wonder why the whale is where it is?

Other allometries

1. The metabolic cost of running (ml O2 g^-1km^-1) = 8.61 * m_b^0.65
2. Mammal brain weight (excluding primates) = 0.01 * m_b^0.70
3. Monkey brain weight = (0.02 to 0.03) * m_b^0.66
4. Ape brain weight = (0.03 to 0.04)* m_b^0.66
5. Brain weight in man = (0.08 to 0.09) * m_b^0.66

Using allometric equations

1. Using 3/4 power scaling
   Have you noticed that for some drugs (an example is neuromuscular blocking agents) per kilogram dosing seems to be wholly appropriate, while for others, giving a dose based on the body weight is inadequate at low body weights (for example, aminophyllin and many antibiotics, administered to children)! Careful consideration may lead you to the conclusion that the initial dose of a neuromuscular blocker may depend on blood volume (which scales with weight) but if the metabolic removal of a drug is important (for example, aminophyllin) then three-quarter power scaling will apply.

   It thus seems reasonable to relate certain drug doses to the 3/4 power of the weight, and not to either weight or surface area. This isn't as difficult as it sounds. The cheapest pocket calculator usually has a square root function and a memory, so if we know the dose for a 70kg person, let's call it D₇₀ and our patient weighs say 32kg, we could work out the relevant dose D₃₂ as follows:

   D₃₂ = D₇₀ * (32/70)^3/4

   This looks formidable but we can easily find the three quarter power of 32/70 as follows:

   1. Cube 32/70:
      • Clear memory and then work out 32/70 ( 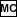32 70 0.457 )
      • Store the result in memory ( )
      • Multiply the result by itself, and then by the value retrieved from memory.
        ( 0.457 0.457 0.209 0.0955 )
   2. Find the fourth root of the result - press square root twice. ( giving the result we want: 0.556)

   You should not go out and apply this willy-nilly for all drugs, and for all people. Body composition and behaviour vary remarkably within the human species, especially at the extremes of size and age. Three quarter power scaling goes a long way towards explaining why we encounter statements in the medical literature about the peculiar doses we need to give to children, and very small or very large adults. If you're dealing with a metabolic variable (such as a drug dose, a clearance, cardiac output, or whatever) think Kleiber!

   Now that you know this, how about taking the per kilogram doses you use for children and comparing them with the per kilogram doses recommended for adults and seeing whether they square up? A really keen person might like to compare veterinary doses of drugs (for example, fentanyl) with human doses.

   The justification for the above formula is that if D₇₀ = a*70^3/4 and D₃₂ = a*32^3/4 then D₃₂ / D₇₀ = (32^3/4) / (70^3/4) which gives us D₃₂ = D₇₀ * (32/70)^3/4.

2. Read "the literature" with caution
   We have already encountered our dimensionally incorrect friends Harris and Benedict. Similar circumspection could perhaps be applied to all reports where for example a metabolic parameter is related to either weight or to surface area. The likelihood of a major difference is probably small when dealing with humans (except at the extreme ranges of body mass) but you should at least feel uncomfortable with information where an empiric index is used.

   For the record, Kleiber reformatted the Harris-Benedict equation (using their data) in a less dimensionally-challenged way:

   • For men: Q = 71.2 * m_b^3/4 * (1 + 0.004(30-y) + 0.010(S-43.4))
   • Women:   Q = 65.8 * m_b^3/4 * (1 + 0.004(30-y) + 0.010(S-43.4))
     
     Where Q is heat production in kcal/day, w = weight in kilograms, y = age in years and S, the specific stature, is height in centimetres / m_b^1/3
   Clearly, it's easier to use the incorrect version, but with modern calculators and computers, we have little excuse.

3. The really good stuff
   The real applicability of scaling will probably only become apparent when we understand what it's all about - why for example as size increases the heart rate slows, in the place of decreasing cardiac size relative to weight. Similar slowing may be intimately associated with the lifespan of the organism, which increases with mass. The lifespan of captive mammals has been found to approximately fit the allometric equation:
   t_life = 11.8 m_b^0.20

   The corresponding equation for birds is

   t_life = 28.3 m_b^0.19

   Obviously these are broad rules, with several exceptions. Most animals seem to survive for about 800 million to a billion heartbeats - humans are exceptional in this regard, as you can easily calculate. We don't know what causes ageing, but it's tantalising that the exponent in the above equations is so close to a quarter. It's not unreasonable to assume that faster metabolisms cause faster metabolic wear-and-tear on cellular structures (mitochondria, telomeres and so on), and that this may give us fundamental insights into ageing.

   Quarter-power scaling has even been reported in plants and microbes! (References: Niklas KJ Am J Bot 1994 81 134 and Hemmingsen AM Rep Steno Mem Hosp 1950 4 1, ex West 1997).

Explanations Please!

In some simple circumstances, we have reasonable explantions for allometric equations. Take the case of pores in the egg of a bird - as the size of the egg varies, so does the thickness of the egshell, and total pore area is accurately adjusted to ensure that evaporative water loss is constant for all eggs (about 15% of weight). Once we examine more complex cases, our logic tends to break down.

Some attractive explanations for allometric equations must be rejected out of hand. For example, if we were to predict that the primary determinant of bone mass was the static load placed on the animal, then the exponent should be 1.33 and not the 1.08 we noted above. It is clear that static loads do not determine bone mass - the important consideration appears to be stresses on the skeleton during movement! It is often easier to reject an explanation based on allometric equations, than to accept it - Karl Popper would be delighted!

"Why three quarters?"

• McMahon (1973)
  This argument is based on engineering of the skeleton. He argues that:
  1. Animals cannot remain isometric with increasing size, as loads would increase more than the ability of the skeleton to withstand such loads;
  2. All proportional changes in bones should be similar, as different maneuvers (running, standing etc) impose different stresses
  3. The critical length (L_cr) at which a column buckles is given by:
     L_cr = k (E/rho)^1/3 d^2/3
     where d is the diameter, E is Young's elastic modulus, and rho is the density of the material. This holds for both hollow and solid cylinders (k differs). In other words, L³ is proportional to d²
  4. If the weight of a limb m_l is proportional to the body weight m_b, then
     m_b is proportional to L * d²
     (as the limb weight is proportional to length (L) times diameter (d) squared)
  5. But by our elastic criteria, L³ is proportional to d², so mass is proportional to L⁴, which is another way of saying that L is proportional to m_b^1/4. Similarly d is proportional to m_b^3/8.
  6. Because work is force * distance, the power output of a muscle is given by
     P_max = maximal tensile stress * area * change in length / time
     Now the maximal tensile stress in a muscle is scale-invariant, as is change in length per unit time. Thus muscle power depends only on cross sectional area. If this area is proportional to d² (a reasonable assumption) then
     P_max is proportional to d², or

     P _max is proportional to (m_b^3/8)²

     which conveniently works out to m_b^3/4

  I would like to see a good critique of this theory, which certainly seems to work in cattle, but the general applicability has been questioned.

  
  

• West et al (1997)
  These authors used an extremely complex argument to achieve the magical three quarters. They use an entirely different tack from that of McMahon - they look at the energy cost of transporting essential materials to where they are needed. Their basic assumptions are that minimal energy is dissipated (not unreasonable) and that terminal capillaries are size-invariant (we know this). Transport is through a space-filling fractal network of branching tubes and the model has fairly general applicability. They argue that:

  1. The metabolic rate is proportional to the flow (Q) through the system, and that at the kth level of branching, Q = N_k.pi.r_k²u_k, where N_k is the number of branches at the kth level, and u_k is the mean flow velocity (averaged over area and time). Specifically, for capillaries, Q = N_c.pi.r_c²u_c.
  2. They assume that capillary radius, length and mean flow (abbreviated r_c, l_c and u_c) are size invariant. If the allometric equation governing the relationship between Q and body mass m_b is Q = k.m_b^a, it follows that N_c scales in proportion to m_b^a. In other words, the number of capillaries scales in proportion to the metabolic rate.
  3. They prove that for minimal energy dissipation, the branching of the network must follow the rules for a self-similar fractal. In this circumstance, the number of branches increases in geometric proportion as their size decreases. If each tube at branching level k branches into n_k smaller ones, then for a self-similar fractal, N_k = n^k ie as k increases so the number of branches increases in geometric proportion. Thus, as the mass increases, so the number of capillaries increases with the logarithm of the mass.
  4. They use the above to prove that a, the exponent of m_b in the allometric scaling equation, is equal to ln(n)/ln(gamma.beta²), where gamma and beta are scale factors that characterise the branching of the system (In general for such systems beta_k = r_k+1/r_k and gamma_k=l_k+1/l_k, but in these circumstances, the values are constant at all levels, and simply referred to as beta and gamma).
  5. Further complex argument (assuming that branching is area-preserving) gives the magic number of a = 3/4. Woops, in mammalian systems, the branching isn't area-preserving, but all is not lost, as yet more complex arguments again give us the magic 3/4 by invoking pulsatile flow as a saviour.

  I have a lot of trouble with the above argument.

  1. The main tenor of the argument seems to be that the three-quarter power is a necessity imposed by the fractal nature of the system, held in place by the necessity to minimise the energy used in distributing nutrients to the tissues. They overlook the fact that the energy required by the pumping action of the heart is a relatively small proportion of total energy expenditure. (Note that as Schmidt-Nielsen details, the oxygen cost of supplying 1 ml of oxygen to the tissues is probably size invariant).
  2. Even more worrying about the above argument is the implied assertion that the nature of the "fuel delivery" system constrains the organism to have a higher metabolic rate than we would expect from the simple necessity to balance energy production and loss (our old friends Sarrus and Rameaux). Guyton's argument that the peripheral tissues regulate cardiac output by their demands (rather than central control) seems to stand in the way of this sort of reasoning, as does the evidence that vessel formation is dictated by the needs of the tissues, rather than the other way around.
  3. The argument overlooks the relationship between an animal and its environment. The major constraint on energy utilisation by an animal is surely whether it is using that energy optimally in relation to its environment. Most animals are not standing around tamely in cages having their metabolisms measured by physiologists - they are interacting with their environment - hunting or escaping, feeding or migrating, shivering or panting, and so on. Any argument that ignores this is surely incomplete by its very nature!

  
  

• Banavar & colleagues
  This argument is also complex - it too is based on the concept of a branching network supplying nutrients, as is that of West. The argument here is much more general, with fewer constraints. They too derive a three quarter exponent by:
  1. Proving that for the most efficient network, blood volume C scales with L^D+1 where L is a parameter of linear size, and D the number of dimensions of the object (3, in our system).
  2. Asserting that blood volume scales with mass;
  3. Proving that metabolic rate (B) scales with L^D
  4. And thus, as mass is proportional to L^D+1 and L is proportional to (metabolic rate)^1/D we get our magic result that metabolic rate is proportional to mass^D/D+1

  Hmm. I'm afraid that despite its apparent greater generality, this argument too is susceptible to the problems we found with West's one.

  
  

• Witting Witting does use an environmental argument, and he too arrives at the magical 3/4 exponent, but only for terrestrial animals that forage in two dimensions. For pelagic ones (that forage in three dimensions) the exponents should be different. Hmm - so far the evidence seems to be in his favour, but we watch eagerly for more hard data. You may wish to check out his web-site where some downloads are available.

  
  

• Nobody
  Nobody seems to have fully considered that an important constraint on animal survival is it's peak capacity for work (rather than its so-called "basal" energy output), although McMahon has touched on this. If you are either a predator or prey, you need to be able to run bloody fast at times, or you will starve or be eaten! Interestingly enough, the principles of symmorphosis here seem to apply to the whole organism. Consider how top-class athletes are continually damaging themselves - ruptured tendons, torn muscles, broken bones and so on seem to be the inevitable concomitants of pushing oneself to the limit - as if the whole organism were designed around these maximum tolerances. (In contrast, there has been much argument that the respiratory system does not fit in with the principle of symmorphosis!) As we have noted above the maximum oxygen consumption of an organism appears to usually be about ten times its basal consumption (some have termed this "factorial aerobic scope"). The question then arises "If the maximum oxygen consumption of an organism is x, does this maximum necessitate some corresponding minimum oxygen consumption (perhaps x/10) that we have graced with the term 'basal oxygen consumption'?" In other words, have we got things the wrong way around? We should carefully consider those organisms with a factorial scope of over 10 (for example, highly trained athletes and dogs, who have a factorial scope of about twenty) and see how they fit into the picture! Have you noticed how smaller dogs seem to live longer than larger ones, apparently defying Kleiber's rules?

References

1. Kleiber M. Physiological Reviews 1947 27 511-541. A brilliant review. Read it!
2. Taylor and Weibel. Respiratory Physiology 1981 44 1-10.
3. Schmidt-Nielsen K, Scaling. Why is animal size so important? Cambridge University Press, 1984. ISBN 0 521 31987 0, ISBN 0 521 26657 2. Get the book. A fascinating read! Much of the above is based on this book.
4. McMahon TA Science 1973 179 1201-4
5. West GB, Brown JH and Enquist BJ. Science 1997 276 122-6.
6. Banavar JR, Maritan A and Rinaldo A. Nature 1999 299 130-2 and Supplementary information at nature.com
7. Heusner. Respiratory Physiology 1982 48 1-12. Arguments in favour of a 2/3 exponent within a species.

Web References
Take a look at:

• A non-technical review of West's work
• Another review of West, with added pretty pictures
• More stuff on West from the New Scientist
• Various more technical comments on West's approach (at Science magazine)
• A review of Banavar's work
• A note on the clinical use of scaling (how it doesn't work too well in estimating hepatic clearances)!
  (Lavé T, Coassolo P, Reigner B. Prediction of hepatic metabolic clearance based on interspecies allometric scaling techniques and in vitro-in vivo correlations. Clinical Pharmacokinetics 36: 211-231, Mar 1999)
• A brief review by Witting of his ecological argument, contrasted with West's approach.